Problema Solution
The center of the circle is at (-3,-2) and its radiusis 7. The chord is 4 and is bisected at (3,1). At what points does the circle cut the y-axis?
Answer provided by our tutors
To find the y-intercepts of the circle, we write the circle's equation in standard form:
(x - (-3))^2 + (y - (-2))^2 = 7^2
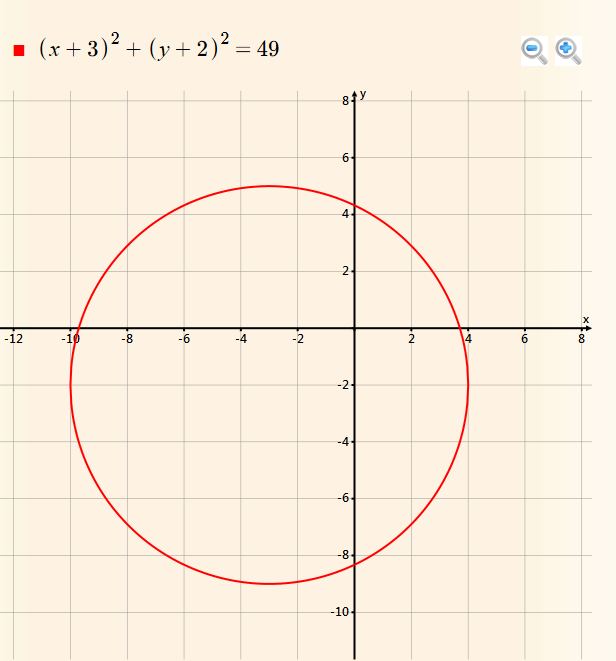
(x + 3)^2 + (y + 2)^2 = 49
The y-intercepts happens when x=0, so we plug x = 0 into the above equation of the circle:
(0 + 3)^2 + (y + 2)^2 = 49
........
click here to see the equation solved for y
........
y1 = 4.32
y2 = -8.32
The y-intercepts of the circle are at (0, 4.32) and (0, -8.32).
Click here to see the graph of the circle (x + 3)^2 + (y + 2)^2 = 49