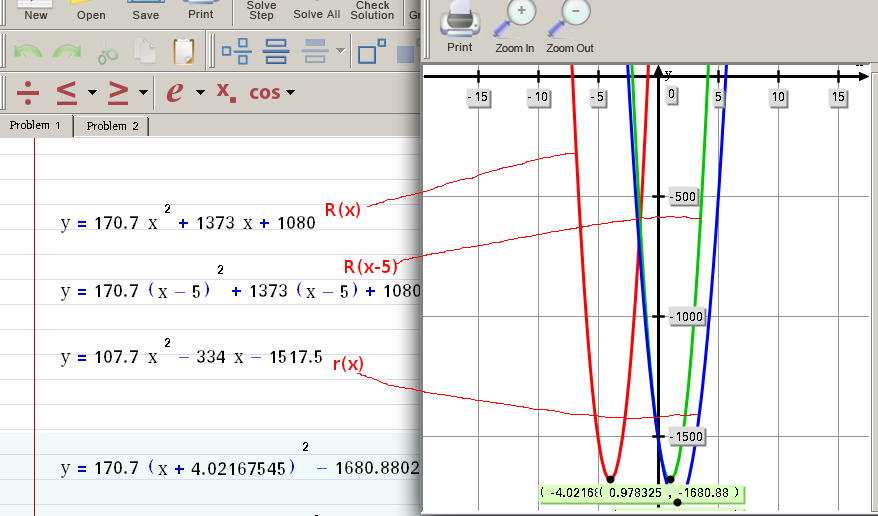
Problema Solution
The revenue is described by the equation: R(x) = 170.7x^2 +1373x + 1080
A. Find R (0) and R (5) and explains what the value represent: R (0) = 170.7*0^2 + 1373*0 + 1080 R (0) = $1,080
The revenue in the year of 2005 was $1,080. R (5) = 170.7*5^2 + 1373*5 + 1080
R (5) = $12,215.50
The revenue in the year of 2010 was $12,212.50.
B. r = R(x-5) r = 170.7(x - 5) ^2 +1373(x - 5) + 1080
r = 107.70x^2 - 334x - 1517.5
C. Find r (5) and explain what this value represents R (x) = 107.70x^2 - 334x - 1517.5
R (5) = 107.70*5^2 - 334*5 - 1517.5 r(5) = -495
If we define the function r(x) = R(x-5), how do we interpret x in that context?
Answer provided by our tutors
A problem submission should stick with a single issue.
If the revenue for R(0) was the year of 2005 and R(5) was revenue for 2010. So, R(x-5) indicates the revenue "5 years earlier" than whatever year 'x' is chosen.
The graph should be used to interpret the contex for 'x't: