Let

a = 10

b = 6

Angle B = 100 degrees

d1 = the shorter diagonal

d2 = the longer diagonal

A = the area

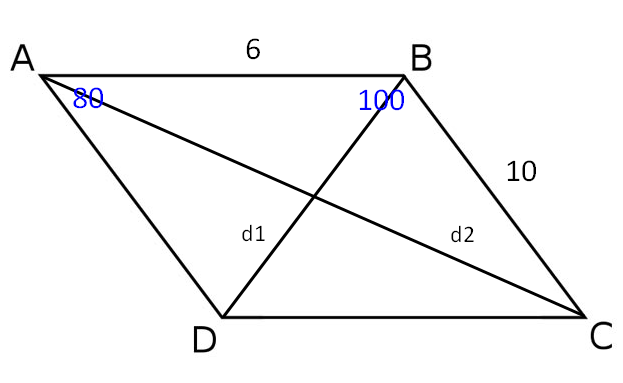
Angle A = 180 - Angle B

Angle A = 180 - 100

Angle A = 80

Using the The Law of Cosines we have:

d1^2 = 10^2 + 6^2 - 2ab cos(Angle A)

d1^2 = 10^2 + 6^2 - 2*10*6*(cos(80))

........

click here to see the equation solved for d1

........

d = 10.73

The length of the shorter diagonal is 10.73.

d2^2 = a^2 + b^2 - 2ab cos(Angle B)

d2^2 = 10^2 + 6^2 - 2*10*6*(cos(100))

........

click here to see the equation solved for d2

........

d2 = 12.52

The area of the parallelogram is:

A = a*b*sin(100)

A = 10*6*sin(100)

........

click here to see the calculation for A

........

A = 59.09

The area of the parallelogram is 59.09.