Problema Solution
The total coast of producing a type of truck is given by C(x)=14000-20x+0.02x(squared), where x is the number of trucks produced. How many trucks should be produced to incur minimum cost?
Answer provided by our tutors
We need to find the minimum of the quadratic function:
C(x) = 14000 - 20x + 0.02x^2
Since the quotient in front of x^2 is 0.02>0 the function has minimum.
click here to see the graph of the function
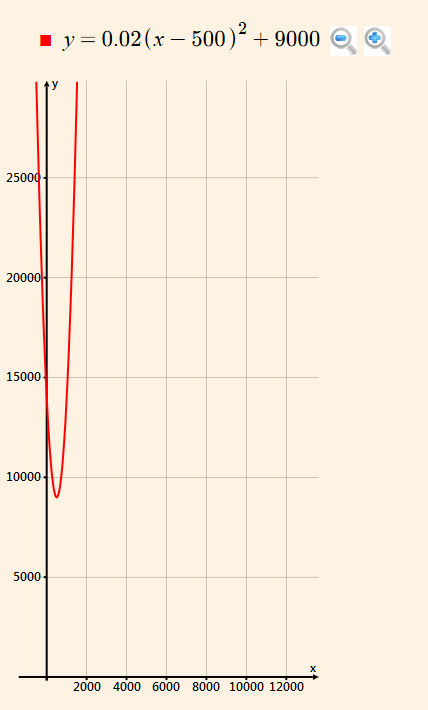
The minimum of the function is in the vertex (- b/2a, c - b^2/(4a)), where a = 0.02, b = -20, c = 14000 (the quotients of the function C(x) = 14000 - 20x + 0.02x^2)
-b/2a = -(-20)/(2*0.02) = 500 trucks
500 trucks should be produced to incur minimum cost.