A Digital View of Numbers

Lecture topic 1: A rational number is a repeating decimal
Calculate the decimal representations of 3/7, 2/6, and 5/6 on the blackboard, and use the results
to explain why the following are true in general:
a. The decimal expansion of the rational number a/b ends in a repeating sequence of digits whose
length cannot exceed 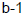(because there are only 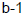possible nonzero remainders.)
b. If the length of the repeating sequence is less than 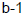, there may be some non-repeating digits
before the repeating sequence starts, but there cannot be more than 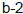non-repeating digits.
c. If the decimal expansion of π has not repeated after 2 trillion digits, that fact does not prove that
π is an irrational number.

Lecture topic 2: A repeating decimal is a rational number.
Here is the standard way to convert a repeating decimal x to a rational number.
Multiply x by the smallest power of 10 (call it 10ⁿ) that moves one copy of the repeating sequence
to the left of the decimal point.
Multiply x by the smallest power of 10 (call it 10^m) that leaves one copy of the repeating sequence
just to the right of the decimal point. Often 10^m is 1.
Now both 10ⁿ x and 10^m x have the same digits to the right of the decimal point, so
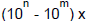is an integer a, and 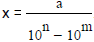. Reduce this fraction to lowest terms .

Apply this process to convert the following decimals to fractions:
0.33333333....
0.83333333....
0.428571428571....

Lecture topic 3: A repeating decimal is a geometric series
An easier, though equivalent, technique for converting a repeating decimal to a fraction is
simply to note that a repeating decimal is shorthand for an infinite geometric series.

For example, x = 0.6363636363...
is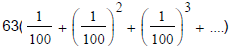
But the sum of the series is 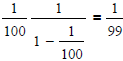and so .

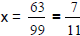Apply this approach to the repeating decimals from topic 2. You will end up doing exactly the
same arithmetic .

Lecture topic 4: Converting hexadecimal integers to decimal integers.
The hexadecimal number system is often used in conjunction with digital computers. The digits 0
through 9 have their usual meaning, and then there are 6 more digits:
A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
By analogy with the meaning of the decimal number 345 as 3 x 10² + 4 x 10 + 5,
the hexadecimal number 3AB represents 3 x 16² + 10 x 16 + 11.
Show how to find the decimal equivalent of CD by hand, then use the Windows calculator in
"scientific" mode to find the decimal equivalent of 2FEFD8

Lecture topic 5: Converting hexadecimal fractions to decimal fractions
Show how to express 3.141592... as an infinite series in powers of
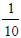
Show how to express 3.243F6A... as an infinite series in powers of
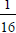
In fact, these numbers both are the start of an infinite series for π.
In hexadecimal notation (10 = "A", 11 = "B"...15 = "F")
π can be approximated as p = 3(base 10) + 0.243F6A(base 16), where the integer part is in
decimal notation but the fractional part is in hexadecimal. By repeatedly multiplying the base 16
fraction (as a 6-digit integer) by A (10 decimal) using the Windows calculator in scientific mode,
show that
10π = 31(base 10) + 0.6A7A24(base 16)
100π = 314(base 10) + 0.28C568(base 16)
1000π = 3141(base 10) + 0.97B610(base 16)

Lecture topic 6: Converting an Euler fraction to a decimal fraction
Euler' s rewrite of Gregory's series is

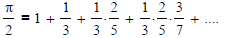
A generalization of this can be used to represent a number as an "Euler fraction".

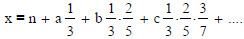
where n is any integer, a < 3, b < 5, c < 7....
Explain the reason for this restriction (which is like a < 10 for decimal digits!)
As shorthand, we can write this as x=n.abc....
Show that with this convention, π = 2.22222....
As a warmup, show how to multiply the decimal number 2.22 by 6, leaving all the digits less than
10. You probably learned to do this in the third or fourth grade.
Next show how to multiply the Euler fraction 2.2 by 10, leaving the result in a form where a < 2.
Then show how to multiply the Euler fraction 2.22 by 10, leaving a < 2 and b < 4

Lecture topic 7: the "spigot algorithm" for computing digits of π
This generalizes what was done in topic 6, but you can use the Windows program Vspigot.exe
(on the course Web site) to automate the tedious process of multiplying by 10 and then making
a, b, c, ... conform to the restrictions. Use the program to show how to start with
π = 2.2222222... and crank out the decimal digits of π one after another.
The program makes it easy to reproduce the table on the first page of the original article on the
spigot algorithm (1995).