Algebraic Expressions
1.3 Algebraic Expressions
A polynomial is an expression of the form:
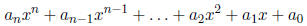
The numbers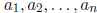 
are called coefficients .
Each of the separate parts, such as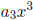 
or
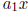, is called a term of the polynomial.
If there is only one term, it is called a monomial. For two terms , it is called
a binomial . For three terms, a
trinomial .
The degree of the polynomial is n: the highest power of x.
To add ( or subtract ) polynomials, we combine like terms (those that have the
same variables raised to the
same powers).
Example: Find the difference (x3 - 4x2 + 6x + 12) - (2x3 + x2 - 4x - 6)
To multiply polynomials, we use the distributive laws . In particular, to
multiply two binomials, we use the
FOIL method.
Example: Multiply (x - 7)(2x + 3)(x - 1)
Special Product and Factoring Formulas
1. Difference of Squares
(A + B)(A - B) = A2 - B2
2. Perfect Squares
(a) (A + B)2 = A2 + 2AB + B2
(b) (A - B)2 = A2 - 2AB + B2
3. Cubing a Sum or Difference
(a) (A + B)3 = A3 + 3A2B + 3AB2 + B3
(b) (A - B)3 = A3 - 3A2B + 3AB2 - B3
4. Sum or Difference of Cubes
(a) A3 + B3 = (A + B)(A2 - AB + B2)
(b) A3 - B3 = (A - B)(A2 + AB + B2)
Examples: Expand the following.
•
•
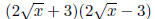
(x3 - 4)2
•
(x2 - 2)3
Factoring Steps
1. Factor out all common factors.
2. See if you can use a special factoring formula .
3. See if you can factor by grouping.
4. Use trial and error.
Examples: Factor the following.
•
8x2 - 24x + 18
•
36x2 - 25
•
x3 - 27
• 2x2 + 11x - 21
•
x3 + 3x2 - x - 3
• (a2 + 2a)2 - 2(a2 + 2a) - 3
To factor expressions with rational exponents , first factor
out, if possible, the smallest power of x.
• Factor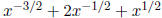 
Its easy to check if you factored correctly. Just multiply back out to double
check.
1.4 Rational Expressions
A rational expression is a fractional expression where both the numerator and
denominator are polyno-
mials.
The domain of any algebraic expression is the set of values that the variable
can be.
So far, we have two things to look for to determine the domain:
•
The denominator can 't be zero. If a value of x makes the denominator zero, we
must exclude it from
the domain.
•
For even powered roots (square roots, fourth roots, etc), whatever is under the
radical must be ≥ 0.
Examples: Find the domains of the following rational expressions.
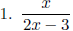
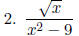
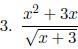
Working with rational expressions is just like working
with fractions.
To multiply rational expressions, factor the numerator and denominator ,
multiply, and then simplify by
cancelling common factors in the numerator and denominator.
To divide rational expressions, multiply by the reciprocal .
To add or subtract rational expressions, you MUST have a COMMON DENOMINATOR
(just like with
fractions).
Examples
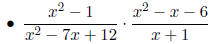
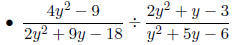
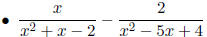
Compound fractions are fractional expressions where the
numerator and/or denominator are themselves
fractional expressions.
Examples:
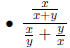
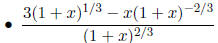
Rationalizing the Denominator or Numerator
As before, rationalizing means to get rid of any radicals. We do this by
multiplying by the conjugate. The
conjugate is usually found by just changing the sign of the second term.
For example, the conjugate of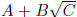 
is
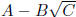. What's the point? When you multiply these two
expressions together you get an expression that has NO radicals:
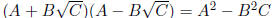
Examples
• What are the conjugates of:
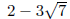
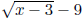
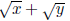
• Rationalize the denominator of
.
•
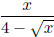Rationalize the numerator of 
.
| Prev | Next |