Discrete Mathematics Exam 1 Study Guide
1. Definitions:
Chapter 1: interrogatory, exclamatory, paradox, statement (proposition), truth
value,
compound statement , logical connectives, truth table, conjunction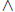 
, disjunction
,
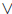implication (conditional) →, hypothesis (antecedent), conclusion (consequent),
bicon-
ditional (equivalence)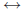 
, negation ',
well-formed formula (wff), tautology, absurdity
(contradiction), DeMorgan' s Laws , exclusive or
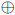, propositional calculus,
argument,
premise (hypothesis), conclusion, valid, proof sequence, rules of equivalence ,
rules of
inference, quantifiers, universal quant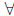ifier 
, predicate, existential
quantifier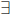 
, scope,
free variable , predicate logic, rules of derivation
Chapter 2: theorem, inductive reasoning, deductive reasoning, counterexample, n
fac-
torial n!, proof, proof by cases (exhaustion), direct proof, even, odd, contrapositive,
contradiction, rational number , perfect square, prime, composite, divides l ,
absolute
value, Principle of Mathematical Induction , basis step, inductive step, PMI
(Principle of
Mathematical Induction), basis step , induction step, induction hypothesis,
conclusion,
proof using PMI, recursive definition, sequence, term, recurrence relation,
Fibonacci
sequence, initial condition, closed- form solution , summation notation , index of
sum-
mation, first-order linear recurrence relation with constant coefficients,
homogeneous,
particular solution, second-order, characteristic equation , characteristic roots
2. Determine whether a sentence is a statement
ex: Los Angeles is the most populous city in the U.S.
3. Determine whether a compound sentence is a compound statement
ex: Dr. Hein is not from Germany, or if he like dogs then he like pets
4. Write a compound statement as an English sentence
ex: If P: The sky is blue and Q: Jupiter had life on it 10,000 years ago, write
P Q in
English
ex: With the same P and Q above, write (P Q) → (P') in English
5. Write an English sentence as a compound statement
ex: If I go to school today, I will ride my bike and not drive my car
6. Determine the truth value of a compound statement
ex: If P is false and Q is true, what is the truth value of (P 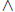Q) → (Q' P)?
7. From a given implication, form the converse, contrapositive and inverse.
ex: For R' → S, construct the converse, the contrapositive and the inverse
8. From a given implication, write the converse, contrapositive and inverse in
an English
sentence
ex: For If I am late, then I drive fast, construct the converse, the contrapositive and
the inverse
9. Write equivalent variations of a conditional.
ex: Write "7 = 3 + 5 only if all dogs bark loudly" in an equivalent form.
10. Use the biconditional properly
ex: What is the truth value of R' 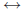S if R is true and S is false
11. Build truth tables of compound propositions (remember the standard order )
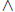ex: Write the truth table for P' (Q' P)
12. Use propositional logic
ex: Show that [(P → Q) 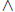Q'] → P'
ex: Prove or disprove: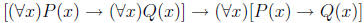 
13. Quantify an open sentence
ex: "Every bat is blind"
ex: "Some dogs have spots"
14. Determine the truth value of a quantified open sentence. (Universe?)
ex: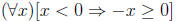 
ex: (y)[y has eight eyes]
15. Write a quantified statement as an English sentence.
ex: Consider the universe of math teachers. If P(x): x has big ears and Q(x): x
writes
with chalk, write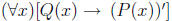 
and
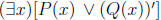in English
16. Prove by contradiction
ex: Show that if x and y are even and odd integers (respectively), then y · (x+y)
is an
odd integer
17. Prove by contraposition
ex: Show that if x is a rational number and y is an irrational number, then x +
y is an
irrational number
18. Disprove by counterexample, etc.
ex: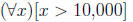 
ex: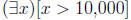 
19. Prove/disprove "proofs" involving quantifiers
ex: There is a largest real number
20. Give an example to show that a certain deduction is false
ex: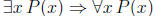 
21. Determine whether statements are equivalent
ex: Are P' (Q' 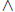P) and P
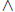Q equivalent?
22. Determine whether a propositional form is a tautology, absurdity or neither
ex: [P 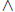(P → Q)]
Q'
23. Determine the validity of an argument
ex: I walk to work or I drive my car. If it rains, I do not walk to work. I
drive my car.
Therefore, it rains.
24.Be able to use the PMI
ex: Show that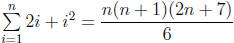 
for all natural numbers n
ex: Show that for all natural numbers n,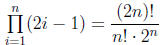 
25. Find the value of a summation
ex: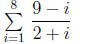 
ex: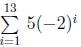 
26. Find the first several terms of a sequence
ex: S(n) = 3n - (-1)n
ex: S(1) = -4; S(2) = -3; S(n) = S(n - 1) - S(n - 2)
27. Find a recursively defined sequence from an "nth-term formula"
ex: S(n) = 2n - 3
28. Find an nth-term formula for a recursively defined sequence (that is, solve
a recurrence
relation); also, check your answer(s)
ex: S(1) = -6; S(n) = 4 + S(n - 1)
ex: S(0) = 5; S(1) = 2; 2 · S(n) = S(n - 1) + S(n - 2)
Notes about the examination:
• The examination should take about an hour.
• Part of the exam is "multiple choice", and part of it is "show your
work". (You will
not need a
).
• The exam will be taken in the Testing Center [see additional
instructions], and will
be open Thursday, September 24 and Friday, September 25.
• Please do all of your work on the white paper | the only thing that
should be on the
examination paper itself is your name.
• No cell-phone calculators will be allowed in the exam room!
• Good luck (if you are depending on luck)!
| Prev | Next |