Factoring

Common Factors :
• Common Factors occur when there is a factor that is common to all terms in the expression
• What are the common factors in the expression below ?


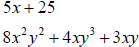
Grouping:
• When you have two or more elements in an expression with common factors, you can group them
together and factor the common factors out
• This doesn't happen all too often in ' real life '
• Does the expression below have common factors? Can you factor by grouping?
y³ − y² + 2y − 2

Factoring Quadratics: ( ax² + bx + c )
• If a = 1
1. The solution will be of the form 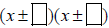, and your goal is to find what goes inside the
boxes along with the signs in front of them
2. Look at the sign of c
− if it is plus then you have the same sign (both plus or both minus). Keep in mind sum
− if it is different then you have opposite signs. Keep in mind difference
3. Identify the factors of c
− find the factors whose sum (or difference) is b
− place these values in the boxes
− be careful with the difference, as the larger value should have the sign of b
• Example. Factor t² − 2t −15
c = –15, so the signs are different
The factors of 15 are 1*15, and 3*5
We are looking for the difference of those factors to be 2, so we choose 3*5
Since we want the difference to be negative , we choose –5 and 3
(x – 5)(x + 3)
• If a ≠ 1
1. Be sure that you can't factor out a constant term
2. Well, there is a method for factoring when it is in this form, but it often causes frustration on
the part of every student, so just use the quadratic formula
3. The formula will yield two values 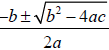, and you factor accordingly

• Example. Factor 20 p² − 23p + 6

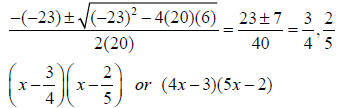
How are these two expressions above the same?

Special Factorizations:
• There are some factorizations that occur more frequently
• The difference of squares is given by A² − B² = (A− B)(A+ B)
• A binomial squared is given by either (A+ B)² = A² + 2AB + B² or (A− B)² = A² − 2AB + B²
• The sum of cubes is given by A³ + B³ = (A+ B)(A² − AB + B² )
• The difference of cubes is given by A³ − B³ = (A− B)(A² + AB + B² )

Pulling it All Together for Polynomials of One Variable (continue in order, stop when factored):
• Look for a greatest common factor, and if possible factor it out
• What degree is the expression?
1. If it is a quadratic (degree 2). How many terms are there?
− If there are two terms in the form (ax² + c) with c negative.
It is the difference of squares
Factor out the coefficient in front of the x² term (a).
The resulting factorization will be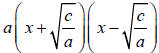
− If there are two terms in the form (ax² + c) with c positive.
You can't factor this in the real number system (you're done)
− If there are two terms in the form (ax² + bx). You should have already taken care of this!
Factor out an x
The resulting factorization will be x(ax + b)
− If there are three terms ( ax² + bx + c ). Is a = 1?
If a = 1, try factoring it (see 'Factoring Quadratics' If a = 1)
If a ≠ 1 use the quadratic formula
Keep in mind this doesn’t have to factor
2. If it is a cubic. How many terms are there?
− If there are two terms and one is constant, it is the sum or difference of cubes
− If there are two terms and one is not constant, you should have already taken care of this!
Factor out the greatest common factor
− If there are three terms with no common factor, you are stuck because it is beyond our
scope for this class
− If there are 4 terms with no common factors, try grouping.
3. If it is of degree higher than 3 and there are no common factors
− We are extending a bit beyond our skill set unless it is of the form presented in (1) or (2)
− In other words, m⁴ −m² − 90 is quadratic in form, and you must think of it as
(m² )² − (m² ) − 90

• Remember, you are not finished factoring just because you complete one step . Be sure it is factored
all the way
• Example. Factor p³ − 2 p² − 9 p +18
It has no common factors
It is of degree 3 (cubic), and has 4 terms, so we will try grouping
p² ( p − 2) −9( p − 2) = ( p² − 9)( p − 2)
Now we are not done, since we still have a quadratic inside
The quadratic has two terms and is the difference of squares
Solution: ( p −3)( p + 3)( p − 2)
• Example. Factor 21x² y + 2xy −8y
Common factor of y: y(21x² + 2x −8)
Quadratic with three terms, use the quadratic formula
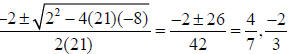
Solution: y(7x − 4)(3x + 2)
• Example. Factor 125a −8a⁴
Common factor of a: a(125 −8a³ )
It is a cubic, with two terms, and one is a constant, so it is the difference of cubes
We use the formula A³ − B³ = (A− B)(A² + AB + B² )
Solution: a(5³ − (2a)³ ) = a(5 − 2a)(5² + 5(2a) + (2a)² ) = a(5− 2a)(25+10a + 4a² )
Now we have the last piece, which is a quadratic with three terms (a not equal to 1)
Use the quadratic formula 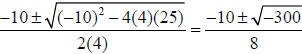. No real roots

Solution: a(5 − 2a)(25 +10a + 4a² )