Factoring and Solving Polynomial Equations by Factoring
Math 0302, Practice Test 5: Factoring and Solving
Polynomial Equations by Factoring
Instructions: Factor the greatest common factor from the following polynomial.
#1 9y2 −15y3 + 33y4
Instructions: Factor each of the following polynomials completely
#2 x2 + 6x + 5
#3 x2 − 2x −15
#4 x2 − 8x + 16
#5 4x3 + 36x2 + 80
#6 98 − 2x2
Instructions: Factor the following polynomial by grouping.
#7 36xz + 9x − 8z − 2
Instructions: Solve the following equations.
#8 x2 − 7x + 10 = 0
#9 12 − 4x = x2
#10 Solve the quadratic equation x2 + 6x – 3 = 0 using the quadratic formula: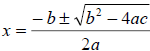
SOLUTIONS
| Instructions: Factor the greatest common factor from the following polynomial. | |
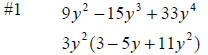 |
3y2 is the largest number that will go into all three terms |
| Instructions: Factor each of the following polynomials completely. | |
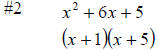
|
x2 + 6x + 5
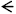 constant constant linear term Since the constant is positive, both binomials take the sign of the linear term. In this case, both binomials will be sums. Note also that the products of the outer terms and the inner terms of the binomial factors combine to the linear term of the trinomial (6x). |
|
x2 – 2x – 15
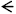 constant constant linear term Since the constant is negative, the binomials will have opposite signs. Note also that the products of the outer terms and the inner terms of the binomial factors combine to the linear term of the trinomial (–2x). |
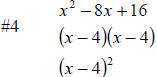
|
x2 – 8x + 16
 constant constant linear term Since the constant is positive, the binomials take the sign of the linear term. In this case, both binomials are differences. Note also that the products of the outer terms and the inner terms of the binomial factors combine to the linear term of the trinomial (–8x). Since the factors are identical, (x-4)(x-4), they can be written as a quantity squared, (x-4)2. |
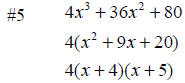
|
4x2 + 36x + 80 The terms of the polynomial share a common factor, 4. Factor the common factor first. x2 + 9x+ 20  constant constant linear term Since the constant is positive, the binomials take the sign of the linear term. In this case, both binomials are sums. Note also that the products of the outer terms and the inner terms of the binomial factors combine to the linear term of the trinomial (9x). |
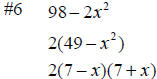 |
The terms of the binomial share a common factor,
2. Factor the common factor first. The binomial factor is a difference of two squares and will factor according to the rule: a2 – b2 = (a + b)(a – b). |
| Instructions: Factor the following polynomial by grouping. | |
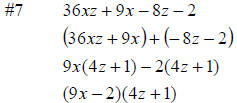 |
This polynomial has four terms, so factor by
grouping. First, rewrite the polynomial as the sum of two binomials . Second, factor out the greatest common factor from each. The greatest common factor of the first binomial is 9x, which yields 9x(4z + 1). The greatest common factor of the second binomial is 2, but factoring out a –2 will create the common binomial (4z + 1). Finally, rewrite the expression as a product of two binomials. |
| Instructions: Solve the following equations. | |
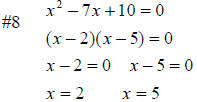 |
Factor the polynomial. Set each factor equal to zero . Solve the two linear equations. |
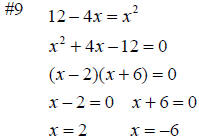 |
Transform the equation so that there is a
polynomial equal to zero. Factor the polynomial. Set each factor equal to zero Solve the two linear equations. |
#10 Solve the quadratic equation x2 + 6x – 3 = 0 using the
quadratic formula: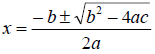
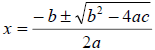 |
Note that a = 1, b = 6, and c = 3. |
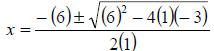 |
Substitute these values into the quadratic formula. |
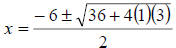 |
Note that the two negatives under the radical create a sum. |
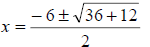 |
The product of 4, 1, and 3 is 12. |
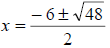 |
The radicand ( number beneath the radical) is 48.
Since 48 is divisible by a perfect square, it can be simplified . To simplify, factor the radicand to two factors including the largest perfect square that will go into it, in this case 16. |
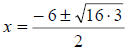 |
|
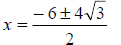 |
The square root of 16 is 4, so rewrite the
radical term as 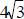 |
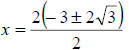 |
Factor the numerator if it has a common factor.
Reduce the common factor with the denominator . |
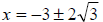 |
These two solutions ,
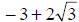 and and
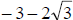 ,
are irrational numbers and cannot ,
are irrational numbers and cannotbe expressed exactly as a decimal . The numbers can, however, be approximated as decimals. x ≈.464 and x ≈ – 6.464. |
| Prev | Next |