Intermediate Algebra Chapter 11 Review

Solve the given equations by completing the square.

1. x² − 4x + 1= 0
2. 2x² + 3x − 4 = 0

Solve the given equations by the method of your choice. Show all
steps in an organized and logical fashion . Give exact answers in
simplified form .

3. 3x² −10 = 65
4. 2x² + 10 = −8
5. (2x − 3)² −7 = 0
6. x² + 2x = 8
7. 2x² = 5x + 3
8. 2x² +7x = −1

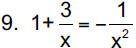
10. 3x² − 2x + 4 = 0
11. x² + x+1= 0
12. x⁴ + 5x² = 36

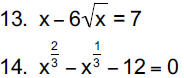
15. (x −1)² + (x −1) + 1= 0

Graph the given quadratic functions . For each function, find the
vertex and the intercepts . Graph the quadratic by using the vertex,
intercepts and other points as needed.

16. f(x) = x² − 4
17. f(x) = (x −1)² + 2
18. f(x) = −(x + 2)² − 4
19. f(x) = x² + 2x − 8
20. f(x) = 2x² − 5x − 3
21. f(x) = x² + 2x + 2

Solve each inequality . Show all steps in an organized and logical
fashion. Write the solution in interval form.

22. 2x² − 5x − 3 ≤ 0
23. x² − 9 ≥ 0
24. 9x² + 3x − 2 > 0

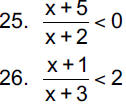
For each of the following problems, follow directions given in the
problem.

27. For each of a-d, find a quadratic equation that has the given
roots . Write the quadratic equation in the form ax² + bx + c = 0.

a. 4,−5
b.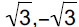
c. 3i,−3i
d. 1+ 2i,1− 2i

28. For each quadratic equation, compute the discriminant. Use the
discriminant to determine the number and kinds of solutions.

a. 2x² − 4x −3 = 0
b. x² = 2x − 6
c. x² = 6x − 9

In the following problems, use your calculator where
appropriate.
29. Use your calculator to find the solutions to the given quadratic
equations, correct to the nearest tenth.

a. 4x² − x −1= 0
b. 1.25x² −.75x − 3.25 = 0

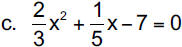
30. Use your calculator to find the minimum or maximum value of
each quadratic function, as appropriate.

a. f(x) = x² − 2x + 3
b. f(x) = 2x² + x − 6
c. f(x) = 3x² − x + 1

For each application problem, use your graphing calculator to graph
the function. Then use the graph to answer the question. If the
answer is not an integer, round it to the nearest tenth.

31. (p. 762, #45) A person standing close to the edge on the top of a
160-foot building throws a baseball vertically upward. The
quadratic function

s(t) = −16t² + 64t + 160

models the balls height above the ground, s(t), in feet, t seconds
after it was thrown.
a. After how many seconds does the ball reach its maximum
height? What is the maximum height?
b. How many seconds does it take until the ball finally hits the
ground?
c. Find s(0) and describe what it means.

32. (p. 734, #66) For this application problem, set up an equation
and solve it showing all steps. You may use your calculator to
approximate the solution only after you have gotten an exact
answer. Round the answer to the nearest tenth.
A rectangular park is 4 miles long and 2 miles wide. How long is a
pedestrian path that runs diagonally across the park?

33. (p.765, #67) The quadratic function

f(x) = −0.018x² + 1.93x − 25.34

describes the miles per gallon of a Ford Taurus driven at x miles
per hour. Suppose you own a Ford Taurus. At what speed should
you drive to maximize the miles per gallon?

34. (p. 790, #11) In 2 years, an investment of $2500 grows to $2916.
Use the compound interest formula
A = P(1+ r)^t
to find the annual interest rate, r.

35. (p. 791, #31) A baseball is hit by a batter. The function

s(t) = −16t² + 140t + 3

models the ball’s height above the ground, s(t), in feet, t seconds
after it was hit. How long will it take for the ball to strike the
ground?

36. (p. 792, #52) The function

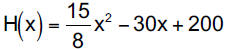
models heart rate, H(x), in beats per minute, x minutes after a
strenuous workout.

a. What is the heart rate immediately following the workout?
b. According to the model, during which intervals of time after
the strenuous workout does the heart rate exceed 110 beats
per minute? For which of those intervals has model
breakdown occurred? Which interval provides a more
realistic answer ? How did you determine this?

Answers:

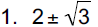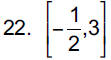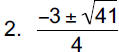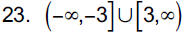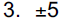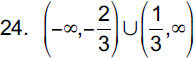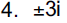	25. ( −5,−2)
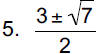	26. ( −∞,−5)∪(−3,∞)
6. −4, 2	27. x2 + x − 20 = 0
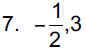	28a. D = 40, two real sol’ns 28b. D = −20, two complex sol ’ns 28c. D = 0, one real sol’n
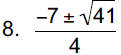	29a. −0.4, 0.6 29b. –1.3, 1.9 29c. –3.4, 3.1
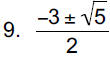	30a. (1,2) 30b. ( −0.2,−6.1) 30c. (0.2,0.9)
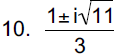	31a. 224 ft. 31b. 5.6 sec 31c. s(0) = 160, The height at time zero is 160 feet .
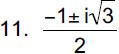	32. 4.5 miles 33. 55 mph
12. ± 2,±3i	34. 8%
13. 49	35. about 8.7 seconds
14. –27,64	36a. 200 bpm
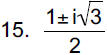	36b. [0,4]∪[12,∞] Model breaks down on the second interval. The heart rate would not start rising after 12 minutes.