Introduction to Analytic Number Theory
0.3 The infinitude of primes
We conclude this chapter with a proof of the infinitude of primes, a result
first proved some two thousand years ago by Euclid.
Theorem 0.2. There are infinitely many primes.
Proof. We give here a somewhat nonstandard proof, which, while not as
short as some other proofs, has a distinctly analytic flavor. It is based on
the following lemma, which is of interest in its own right.
Lemma 0.3. Let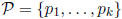 
be a finite set of primes, let
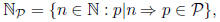
i.e., 
is the set of positive integers all of whose prime factors belong to
the set P (note that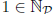 
), and let
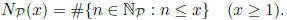
Then there exist constants c and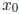 
(depending on P) such that
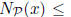
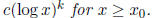
Proof. Note that
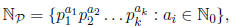
and that by the Fundamental Theorem of Arithmetic each element in
corresponds to a unique k-tuple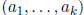 
of nonnegative integers. Thus,
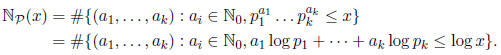
Now note that the inequality
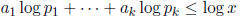implies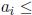 
for each i. Hence, for each
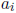there are at most
[ log x/ log 2] + 1 choices, and the number of tuples
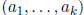counted in
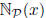is therefore
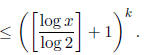
If we now restrict x by x ≥ 2, then [ log x/ log 2] + 1 ≤ 2 log
x/ log 2, so the
above becomes
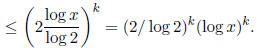
This gives the asserted bound for
with c = (2/ log
2)k and 
.
With this lemma at hand, the infinitude of primes follows easily: If
there were only finitely many primes, then we could apply the lemma with
P equal to the set of all primes and, consequently, the set of all positive
integers, so that = [x] for all x ≥1. But the lemma would give
the bound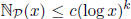 
for all x ≥2 with some constant c, and since
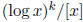tends to zero as x → ∞, this is incompatible with the equality
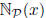= [x].
0.4 Exercises
0.1 Show that there exist arbitrarily large intervals that are free of primes,
i.e., for every positive integer k there exist k consecutive positive integers
none of which is a prime.
0.2 Let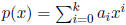 
be a polynomial with integer coefficients
and
of degree k ≥1. Show that p(n) is composite for infinitely many integers
n.
Remark: With "composite" replaced by "prime", the question becomes
a famous problem that is open (in general) for polynomials of
degree at least 2. For example, it is not known whether there are
infinitely many primes of the form p(n) = n2 + 1.
0.3 Call a set of positive integers a PC-set if it has the property that
any pair of distinct elements of the set is coprime. Given x ≥ 2,
let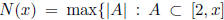 
, A is a PC-set }, i.e., N(x) is the
maximal number of integers with the PC property that one can t
into the interval [2, x]. Prove that N(x) is equal to π(x), the number
of primes ≤ x.
0.4 A positive integer n is called squarefull if it satisfies (* )
.
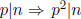(Note that n = 1 is squarefull according to this definition, since 1 has
no prime divisors and the above implication is therefore trivially true.)
(i) Show that n is squarefull if and only if n can be written in the
form n = a2b3 with a, b ∈ N.
(ii) Find a similar characterization of "k-full" integers, i.e., integers
n ∈ N that satisfy (* ) with 2 replaced by k (where k ≥ 3).
0.5 Let be a finite set of primes, let
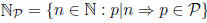
i.e., is the set of positive integers all of whose prime factors belong
to the set P (note that 1 2 ), and let
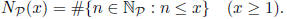
In Lemma 0.3 we showed that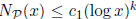 
for a suitable constant
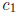(depending on the set P, but not on x) and for all sufficiently
large x, say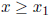 
. Prove that a bound of the same type holds in the
other direction, i.e., there exist constants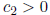 
and
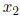, depending on
P, such that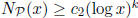 
holds for all
.
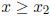| Prev | Next |