Inverse Functions
DEFINITION: If the functions f and g satisfy
the two conditions
g(f(x)) = x for every x in the domain of f
f(g(y)) = y for every y in the domain of g
(*)
then we say that f and g are inverses. Moreover,
we call f an inverse function for g and
g an inverse function for f.
NOTATION: The inverse of a function f is commonly
denoted by f-1.
So, we can reformulate (*) as
f-1(f(x)) = x for every x in the domain of f
f(f-1(x)) = x for every x in the domain of f-1
1. Let f(x) = x3, then
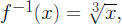since
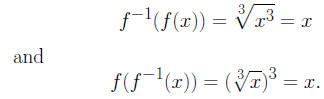
2. Let f(x) = x3 + 1, then
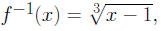
since
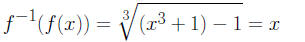
and
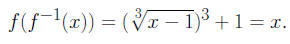
3. Let f(x) = 2x, then
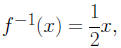since
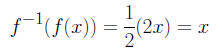
and
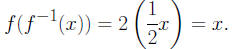
4. Let f(x) = x, then f-1(x) = x, since
f-1(f(x)) = x
and
f(f-1(x)) = x.
5. Let f(x) = 7x + 2, then
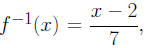
since
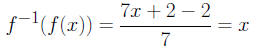
and
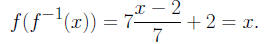
IMPORTANT:
domain of f-1 = range of f
range of f-1 = domain of f
1. Let
,
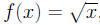then f-1(x) = x2, x≥0.
2. Let
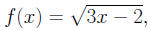then
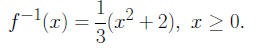
3. Let
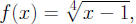then
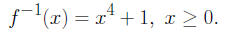
4. Let
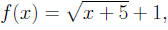then
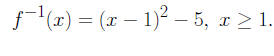
THEOREM (The Horizontal Line Test ): A
function f has an inverse function if and only if
its graph is cut at most once by any horizontal
line .
1. The functions
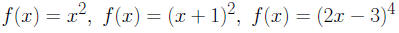
are not invertible.
2. Let f(x) = x2, x≥0. Then
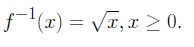
3. Let f(x) = x2, x≥2. Then
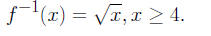
4. Let f(x) = x2, x < −3. Then
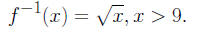
5. The function f(x) = x2, x > −1 is not
invertible.
THEOREM: If f has an inverse function f-1,
then the graphs of y = f(x) and y = f-1(x) are
reflections of one another about the line y = x;
that is, each is the mirror image of the other with
respect to that line .
THEOREM: If the domain of a function f is an
interval on which f'(x) > 0 or on which f'(x) <
0, then f has an inverse function.
1. The function f(x) = x5+x+1 is invertible,
since f'(x) = 5x4 + 1 > 1.
THEOREM: Suppose that f is a function with
domain D and range R. If D is an interval and f
is continuous and one-to-one on D, then R is an
interval and the inverse of f is continuous on R.
THEOREM( Differentiability of Inverse Functions):
Suppose that f is a function whose domain
D is an open interval, and let R be the
range of f. If f is differentiable and one -to-one
on D, then f-1 is differentiable at any value x
in R for which f'(f-1(x)) ≠ 0. Furthermore, if
x is in R with f'(f-1(x)) ≠ 0, then
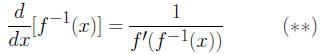
COROLLARY: If the domain of a function f is an
interval on which f'(x) > 0 or on which f'(x) <
0, then f has an inverse function f-1 and f-1(x)
is differentiable at any value x in the range of f.
The derivative of f-1 is given by formula (**).
| Prev | Next |