Linear Systems
1. Solve the following systems of equations below.
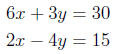
Answer: (11/2,−1)
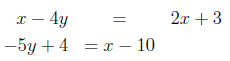
Answer: (−71, 17)
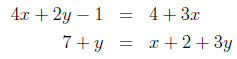
Answer: Any pair of the form (5 − 2y, y). These two equations represent
the same line .
2. Give an example of a linear system of equations with no solution in
which at least one of the lines has slope equal to −1/3.
Answer.
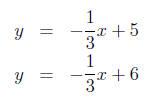
3. New vehicles typically depreciate the minute you drive them off the
lot and then continue to depreciate gradually as time goes by. While
this depreciation is typically not quite linear , we will assume that it
it for purposes of this problem. Let n be the number of years passed
since purchase of the vehicle and denote by VA, VB, and VC the values
of vehicles of each of the three models after n years have passed.
| Model | Price | Initial Depreciation | Depreciation per year |
| A | 25000 | 4800 | 750 |
| B | 32500 | 6100 | 1275 |
| C | 35000 | 7000 | 1525 |
(a) Determine three equations relating each of VA, VB, and VC to n.
Answer.
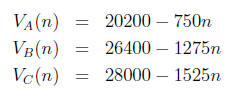
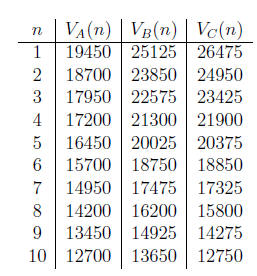
(b) Use your calculator to generate a table that gives the number of
years passed and the values of vehicles of each of the three models
for ten years.
Answer.
(c) Use your calculator to graph the three equations on the same axes
(i.e., graph the system of equations ).
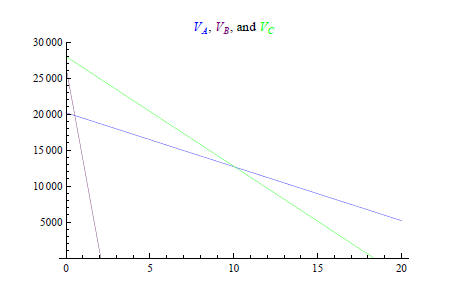
(d) Over what (roughly) time range is a model A vehicle worth more
than either of the other two ? Answer the same questions for model
B and model C vehicles.
Answer A is most valuable after year 11.8095. B is most valuable
between years 6.4 and 11.8095. C is most valuable prior to year
6.4.
(e) Calculate the intersection points of the equations in the system.
Answer. VA and VB intersect at the point (11.8095,
11342.9);
VA and VC intersect at the point (10.0645, 12651.6); VB
and VC
intersect at the point (6.4, 18240)
4. Jill leaves Boston at noon, traveling west at a constant speed of 55 miles
per hour; Bob leaves Boston three hours later, traveling at a constant
speed of 60 miles per hour.
(a) If DJ and DB represent the distances each person
has traveled in
t hours, write equations that relate DJ and DB to t.
Answer. Letting t be the number of hours past 3:00,
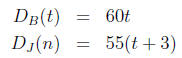
(b) If Bob has been on the road for four hours, how long has Jill been
on the road?
Answer. Seven hours
(c) Graph the equations from part (a) on the same set of axes.
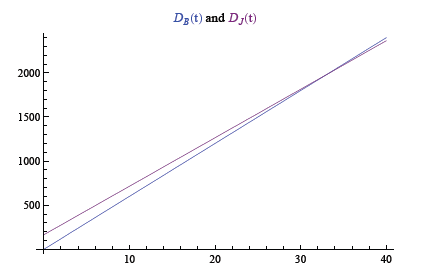
(d) Determine where Bob will overtake Jill, that is, determine both
how long it will take and how far West of Boston will they be
when it happens.
Answer. Bob will overtake Jill 33 hours after his departure, when
they are 1980 miles into their trip.
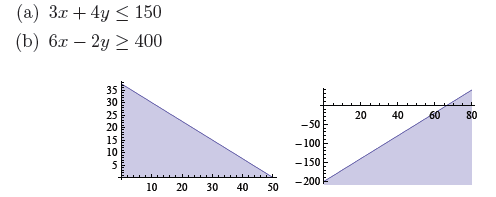
5. Graph (on separate graphs) each of the following inequalities
6. Let
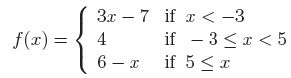
(a) Compute f(−10), f(−3), f(0), f(5), and f(12).
Answer. −37, 4, 4, 1, and −6, respectively.
(b) Graph y = f(x).
7. Let GTMS be the tax on people in Massachusetts who file under the
category “Married/separate” under the graduated tax plan outlined on
page 179 and x be the taxable income of such people. Let FTMS be the
tax on such people under a flat tax plan with a flat tax rate of 5.7%.
(a) Use the information in Table 3.5 in the text (bottom
of page 167)
to express GTMS as a function of x.
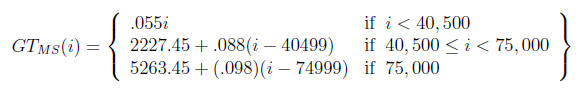
(b) Make an input-output table for the function GTMS
using incomes
ranging from 0 to $100,000 in $10,000 increments.
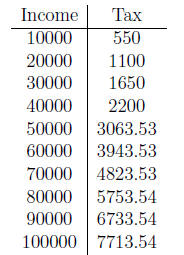
(c) Make a graph that shows GTMS and FTMS
on the same set of
axes, where FTMS is the flat tax at a 5.7% rate on income.
(d) At what income does one pay the same tax regardless of
the tax
plan?
Answer. $ 43,111.80
Extra.
8. Consider the function s(x) defined below
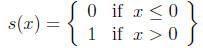
(a) Sketch a graph of this function. This function is
sometimes called
a “step” function because of the appearance of its graph.
(b) Modify s(x) to get a function whose graph is a step
that is twice
as high as the step in s (x).
Answer. 2s(x) or s(x) + 1
(c) Modify s(x) to get a function whose graph is a step
that is two
units further to the right as the step in s(x).
Answer. s(x − 2)
9. If A is a set of numbers, the function
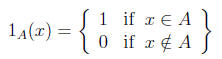
is called the indicator function of A. Explain how your
calculator uses
indicator functions in graphing piecemeal functions.
10. Let A and B be sets of functions. Show that
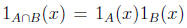
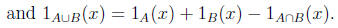
11. Write a formula for the function whose graph is below
using indicator
functions.
| Prev | Next |