MATH 122 Final Exam Review
The final exam for MAT120 and MAT122 will consist of 30
multiple choice questions and 5 open-ended
questions. The exam itself will cover six categories: General function
understanding, linear functions,
quadratic functions, exponential functions , logarithmic functions, and rational
and radical functions. Sample
questions for each topic are given below and are not to be considered identical
to those found on the exam.
A. General function understanding,
- find function values (input and output) using graphs, tables, or algebra
A1. a) Given f (x) = 2x2 -15 find f(10), and find f(-10).
b) Given f (x) = 2x2 -15 , find x, such that f(x) = 3.
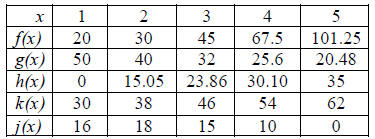
c) Using the table in question A4, find k(3).
d) Using the table in question A4, find x such that k(x)=38.
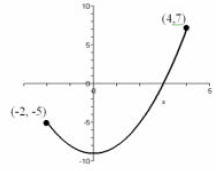
e) Using the graph in A3, find f(0).
f) Using the graph in A3, find x such that f(x)=0.
find the output of a composition of functions using
graphs, tables or algebra
A2. Given f (x) = 2x2 -15 and 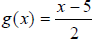 find f (g
(13)) .
find f (g
(13)) .
- determine domain and range of a function using graphs, tables, or algebra
A3. Determine the domain and range of f:
- generate a ‘stat plot’ on your calculator using given
data
- generate a regression function on your calculator using given data
A4. Identify each type of function:
- find the average rate of change between two points on a
function.
A5. Find the average rate of change between h(2) and h(4) in A4.
- work with rules of exponents – give all exponents as positive values .
A6. Simplify:
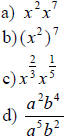
- find the inverse of a function and interpret the meaning
in real -world terms
A7. If f (x) = 150 + 700x find f -1 (x).
A8. If f(x) is a function that gives total cost of renting an apartment through
the first x months of a year,
what does f -1 (4350) = 6 mean?
B. Linear functions:
- identify a linear function based on analysis of constant rate of change
B1. In problem A4, which function(s) is/are linear? How can you justify your
response?
- solve linear equations for a specified variable
B2. Solve 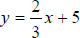 for x.
for x.
- simplify linear expressions
B3. Simplify 2(x+3) – 5(2x-7)
- find the y- intercept and slope of a linear relationship
B4. Find the slope and y-intercept of 5x + 3y = 21
- find a linear function given two points on the function
B5. Give, in y=mx+b form, the equation of the line passing through (-3, 2) and
(5, 7)
- find a linear function given a point and a slope
B6. Give, in y=mx+b form, the equation of the line passing through (-3, 2) with
a slope of -3.
- find the intersection of two linear functions and interpret the meaning
B7. Solve f(x) = g(x) given f(x) = 2x – 7 and g(x) = 5x + 5
B8. Use your graphing calculator to find when the
population will reach 20,000 given that population as a
function of time (t, in years since 2000) is given by P(t) = 32375 – 4500t
- interpret meaning of an answer in real- world terms
B9. What does P(3.5) = 16625 mean with P(t) given in question B9?
C. Quadratic functions:
- identify a quadratic function
C1. In the table for A4, which function(s) is/are quadratic? How can you support
your answer?
- solve quadratic equations by graphing, the quadratic formula, and factoring
C2. Solve 2x2 - 7x = 15 for x by factoring, graphing and the quadratic formula.
C3. Solve 8x2 + 6x + 2 = 0 for x using the quadratic formula. Simplify your
answer.
- perform the indicated operations and simplify the quadratic expressions
C4. Simplify:
a) -2(x2-2x+5) – 3(x2+2x-7)
b) (2x-3)(3x+7)
- find the y-intercept (vertical intercept) of a quadratic function
C5. What is the y-intercept (vertical intercept) of f (x) = 2x2 - 7 x -15 ?
- interpret meaning of an answer in real-world terms
C6. If h(t) = -16t 2 + 40t + 80 represents the height of a ball (above the
ground) thrown from a roof as a
function of time (in seconds), what does h(2)=96 mean?
C7. When will h(t) = 24? What will that mean?
C8. When will the ball hit the ground? How did you find the answer?
- find the vertex and zeros of a parabola and interpret the meaning in context
C9. Find the vertex of h(t). What is the meaning of this in the context of
question C6?
- perform operations on complex numbers (including solutio ns to quadratic
equations)
C10. Simplify:
a) 3i(5- 2i)
b) (3 + i) - (2 - 3i)
c) (3 + i)(2 - 3i)
D. Exponential functions:
- identify an exponential function
D1. In the table for A4, which function(s) is/are exponential? How can you
support your answer?
- solve exponential equations by graphing or using algebra. Round to the nearest
0.001.
D2. Solve for x:
![]()
- find the y-intercept (vertical intercept) of an exponential function
D3. What is the meaning of a and b in f (x) = a · bx
D4. What is the y-intercept of f (x) = 300(1.15)x where f(x) is the population
of a city x years since
2000. What does it mean?
- apply meaning to the base of an exponential function.
D5. What does the 1.15 mean in question D4? What is the growth rate as a
percentage?
- find the inverse of an exponential function
D6. Find f -1 (x) for the function in D4.
E. Logarithmic functions:
- identify an logarithmic function
E1. In the table for A4, which function(s) is/are logarithmic? How can you
support your answer?
- solve logarithmic equations by graphing or using algebra
E2. Solve 3 + log(120 – x) = 5 for x.
- simplify logarithmic expressions
E3. Write the following as a sum, difference or multiple of logarithms
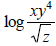
E4. Rewrite the following as the logarithm of a single quantity.
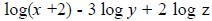
E5. True or False?
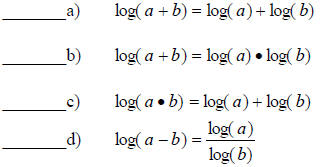
- determine the domain and range of a logarithmic function
E6. What is the domain and range of:
a) f (x) = ln( x)
b) f (x) = log( x -1)
- convert equations between logarithmic and exponential forms
E7. Convert 4x = 1250 into logarithm form.
- apply the change of base formula
E8. Find 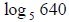
F. Rational and radical functions :
- solve rational and radical equations by graphing or using algebra
F1. Solve 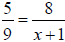 for x.
for x.
F2. Solve 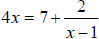 for x.
for x.
F3. Solve 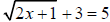 for x.
for x.
- simplify rational and radical expressions
F4. Simplify 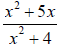
F5. Simplify 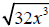
- determine vertical asymptotes of rational functions
F6. Given 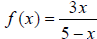 :
:
a. Draw the complete graph of this function.
b. What is the trend? How does the graph demonstrate this trend?
c. Write the equation of the vertical asymptote.
d. What is the input that results in an output value of 9?
F7. Determine the vertical asymptote(s) of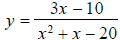
| Prev | Next |