MATH 145: Homework Solutions #6
1. Brualdi 6.2
Find the number of integers between 1 and 10,000 inclusive which are not
divisible by
4,6,7, or 10.
Answer:
Let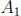 
be the set of integers between 1 and
10,000 that are divisible by 4, 
be the
set of integers between 1 and 10,000 that are divisible by 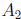6,
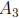be the set of integers
between 1 and 10,000 that are divisible by 7 and let
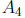be the set of integers between
1 and 10,000 that are divisible by 10. Then by the inclusion-exclusion principle
the
number of integers between 1 and 10,000 inclusive which are not divisible by
4,6,7, or
10 is
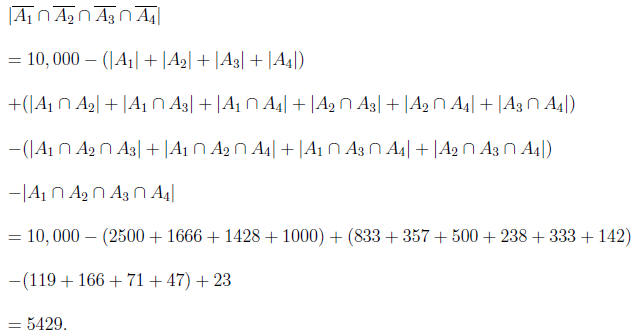
because:
2. Brualdi 6.3
Find the number of integers between 1 and 10,000 which are neither perfect
squares
nor perfect cubes.
Answer:
Let S = {1, 2, ..., 10000} be the set of all integers between 1 and 10,000. Then
|S| =
10000. Let be the set of all perfect squares in S . Then
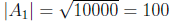since
all integers less than 100 and their perfect squares are in S . Let 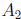be the set
of all
perfect cubes in S . Then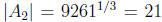 
since 9261 is the
largest number that
is a perfect cube in S . Now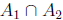 
are integers in
S that are both perfect squares
and perfect cubes. Therefore if n is in 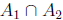, and
the prime factorization of n is
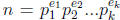then each exponent 
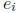is divisible by 6. That is 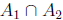are integers
in S that are 6 th powers of an integer . The largest integer which is 6th power
in S is
4096. so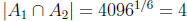 
.
Therefore by the inclusion-exclusion principle we have the number of integers
between
1 and 10,000 which are neither perfect squares nor perfect cubes is
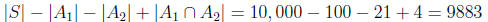
3. Brualdi 6.7
Determine the number of solutions of the equation
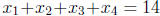in
non-negative
integers 
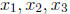and
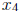not exceeding 8.
Answer:
Let S be the set of all non- negative integral solutions of the equation
.
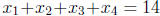Then, the number of non-negative integral solutions of the given equation
is ,
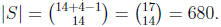
Let the set consist of solutions in S for which
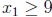We make a change of
variable ,
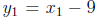to get|| which is the same as the number of non-negative solutions
of
the equation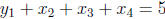 
. Therefore
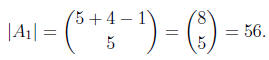
Similarly, if we let
be the set of solutions in S for
which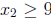 
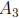, be the set of
solutions in S for which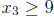 
and
be the set of solutions in S for which
,
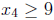we get
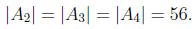
The set 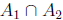consists of solutions in S which have
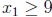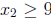and . Let
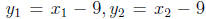. Then, |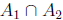| is the same as the non-negative
integral
solutions of the equation
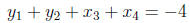
Thus, |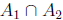| = 0. Similarly, we can easily verify that
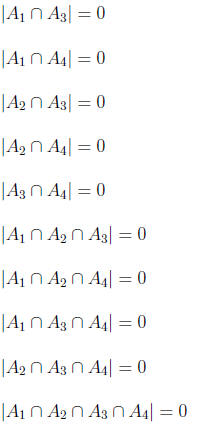
By inclusion-exclusion principle we get that the number of
solutions of the equation
in non-negative integers
and
not exceeding
8 is
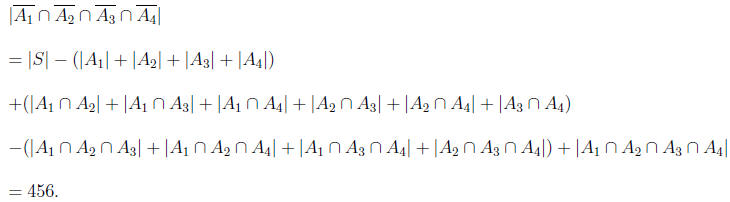
(It is quite obvious that the sets
, . . . , are
disjoint because if two numbers are
greater than 8, then the sum of them together with other non-negative integers
exceeds
14. Thus 680 − 4 × 56 = 456.)
| Prev | Next |