Math Glossary

Base—a number used as a repeated factor in an exponential expression. In 85, 8 is the base number.
Base 10—see Decimal.
Binary system —one of the simplest numbering systems. The base of the binary system is 2, which means
that only the digits 0 and 1 can appear in a binary representation of any number.
Circumference—the distance around the outside of a circle.
Composite number—any integer that can be divided evenly by a number other than itself and 1. All numbers
are either prime or composite.
Counting numbers—include all whole numbers, with the exception of 0.
Decimal—a number in the base 10 number system. Each place value in a decimal number is worth ten times
the place value of the digit to its right.
Denominator —the bottom number in a fraction. The denominator of 1/2 is 2.
Diameter—a chord that passes through the center of the circle and has endpoints on the circle.
Difference—the result of subtracting one number from another.
Divisible by—capable of being evenly divided by a given number, without a remainder.
Dividend—the number in a division problem that is being divided. In 32 ÷ 4 = 8, 32 is the dividend.
Even number—a counting number that is divisible by 2.
Expanded notation —a method of writing numbers as the sum of their units (hundreds, tens, ones, etc.).
The expanded notation for 378 is 300 + 70 + 8.

Exponent—a number that indicates an operation of repeated multiplication. For instance, 3⁴ indicates that
the number 3 should be multiplied by itself 4 times.
Factor—one of two or more numbers or variables that are being multiplied together.
Fractal—a geometric figure that is self-similar; that is, any smaller piece of the figure will have roughly the same
shape as the whole.
Improper fraction—a fraction whose numerator is the same size as or larger than its denominator.
Improper fractions are equal to or greater than 1.
Integer—all of the whole numbers and negatives too. Examples are −3, −2, −1, 0, 1, 2, and 3. Note that integers
do not include fractions or decimals.
Multiple of —a multiple of a number has that number as one of its factors; 35 is a multiple of 7; it is also a
multiple of 5.
Negative number —a real number whose value is less than zero.
Numerator —the top number in a fraction. The numerator of 1/4 is 1.
Odd number—a counting number that is not divisible by 2.
Percent—a ratio or fraction whose denominator is assumed to be 100, expressed using the % sign; 98% is equal
to 98/100.
Perimeter—the distance around the outside of a polygon.
Polygon—a closed two-dimensional shape made up of several line segments that are joined together.
Positive number—a real number whose value is greater than zero.
Prime number—a real number that is divisible by only two positive factors: 1 and itself.
Product —the result when two numbers are multiplied together.
Proper fraction—a fraction whose denominator is larger than its numerator. Proper fractions are equal
to less than 1.
Proportion—a relationship between two equivalent sets of fractions in the form
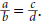
Quotient—the result when one number is divided into another.
Radical —the symbol used to signify a root operation.
Radius—any line segment from the center of the circle to a point on the circle. The radius of a circle is equal
to half its diameter.
Ratio —the relationship between two things, expressed as a proportion.
Real numbers —include fractions and decimals in addition to integers.
Reciprocal—one of two numbers which, when multiplied together, give a product of 1. For instance, since
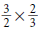is equal to 1, 3/2 is the reciprocal of 2/3.
Remainder—the amount left over after a division problem using whole numbers. Divisible numbers always
have a remainder of zero .
Root ( square root )—one of two (or more) equal factors of a number. The square root of 36 is 6, because
6 × 6 = 36. The cube root of 27 is 3 because 3 × 3 × 3 = 27.
Simplify terms —to combine like terms and reduce an equation to its most basic form.
Variable —a letter, often x, used to represent an unknown number value in a problem.
Whole numbers—0, 1, 2, 3, and so on. They do not include negatives, fractions, or decimals.