Matrix Methods Syllabus
COURSE INFORMATION
Course Description: Matrices and matrix algebra,
determinants, systems of linear equations,
Gaussian elimination , eigenvalues and eigenvectors, linear transformation ,
applications in science
and engineering.
Course Prerequisites : Math 2414 or concurrent enrollment
Student Learning Outcomes: Upon completion of this
course, students should be able to do the
following:
• Perform basic matrix operations including row reduction , transpose, finding
the inverse
and finding the determinant.
• Solve systems of linear equations using substitution, Gaussian elimination,
Cramers rule
and inverse matrices.
• Find eigenvalues and eigenvectors as well as understanding their properties
and importance
to matrix theory and applications.
• Understand the basic properties of Euclidean space including linear
independence, dimension,
rank, orthoganality, norm and projection.
COURSE CONTENT
Required Text:
Bronson, Richard. Matrix Methods , An Introduction , 2nd edition, Academic Press,
1991.
ISBN: 978-0121352516
List of Course Topics: The following is a detailed
list of the sections from your textbook. Chapters
one through five will be covered in detail and selected topics will be chosen
from the remaining
chapters.
Chapter 1. Matrices
Section 1.1: Basic Concepts
Section 1.2: Operations
Section 1.3: Matrix Multiplication
Section 1.4: Special Matrices
Section 1.5: Submatrices and Partitioning
Section 1.6: Vectors
Section 1.7: The Geometry of Vectors
Chapter 2. Simultaneous Linear Equations
Section 2.1: Linear Systems
Section 2.2: Solutions by Substitution
Section 2.3: Gaussian Elimination
Section 2.4: Pivoting Strategies
Section 2.5: Linear Independence
Section 2.6: Rank
Section 2.7: Theory of Solutions
Chapter 3. The Inverse
Section 3.1: Introduction
Section 3.2: Calculating Inverses
Section 3.3: Simultaneous Equations
Section 3.4: Properties of the Inverse
Section 3.5: LU Decomposition
Chapter 4. Determinants
Section 4.1: Introduction
Section 4.2: Expansion by Cofactors
Section 4.3: Properties of Determinants
Section 4.4: Pivotal Condensation
Section 4.5: Inversion
Section 4.6: Cramer’ s Rule
Chapter 5. Eigenvalues and Eigenvectors
Section 5.1: Definitions
Section 5.2: Eigenvalues
Section 5.3: Eigenvectors
Section 5.4: Properties of Eigenvalues and Eigenvectors
Section 5.5: Linearly Independent Eigenvectors
Section 5.6: Power Methods
Chapter 6. Real Inner Products
Section 6.1: Introduction
Section 6.2: Orthonormal Vectors
Section 6.3: Projections and QR-Decomposition
Section 6.4: The QR-Algorithm
Section 6.5: Least- Squares
Chapter 7. Matrix Calculus
Section 7.1: Well-Defined Functions
Section 7.2: Cayley-Hamilton Theorems
Section 7.3: Polynomials of Matrices – Distinct Eigenvalues
Section 7.4: Polynomials of Matrices – General Case
Section 7.5: Functions of a Matrix
Section 7.6: The Function eAt
Section 7.7: Complex Eigenvalues
Section 7.8: Properties of eA
Section 7.9: Derivatives of a Matrix
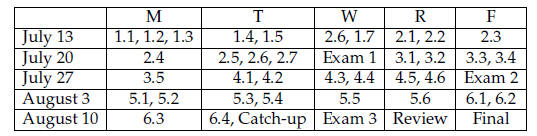
COURSE TIMELINE
Tentative Schedule: This schedule should give you a
rough idea of the pace of the course. Due to
the accelerated nature of summer courses , you will be expected to cover a great
deal of material
in each class, and content will build quickly. It is extremely important to stay
current with course
topics.
COURSE EVALUATION
Homework: You will have assigned homework every
night. Due to the accelerated timeline of
the course and the amount of material to be covered, you MUST stay on top of
your homework in
order to succeed in this course. Homework will be collected two class days after
assigned unless
otherwise announced in class. For submission, fold homework lengthwise (into a
4” ×11”) and place
on the teaching podium BEFORE CLASS BEGINS. Late homework will not be accepted.
In-Class Exams: You will have three in-class exams,
tentatively scheduled for 22 July, 31 July,
and 12 August. As per the technology policy, no technological assistance will be
available during
exams.
Final Exam: You will have a comprehensive final
exam during the regularly scheduled class on
Friday, 14 August.
Grading: Grades will be computed as follows:
| Homework and Quizzes 10% In-Class Exams 60 % Final Exam 30% |
IMPORTANT DATES
| July 13 Classes begin July 16 Census Date July 31 Last day to drop or withdraw from a course or courses August 14 Final exams |
INSTRUCTOR’S POLICIES
Make-ups: Make-ups for documented absences that are
required as part of a UT Tyler obligation
(e.g., athletes participating in an event, participation in a debate contest,
etc.) or for religious observation
will be granted. For all make-ups of this type, documentation and prior
notification of
at least one week are required. All other make-ups will be granted only in
extreme circumstances
and solely at Dr. Graves’s discretion.
Technology Policy: No calculators, PDAs, or
computers will be allowed on exams. Use of Mathematica
or other software may be helpful in checking homework answers, but credit will
only be
given for homework showing legible handwritten work.
UNIVERSITY POLICIES
For University policies concerning Students’ Rights and
Responsibilities, Grade Replacement/Forgiveness,
State-Mandated Course Drop Policy, Disability Services, Student Absence due to
Religious Observance,
Student Absence for University-Sponsored Events and Activities, and the Social
Security
and FERPA Statement please see:
| Prev | Next |