Number Systems

The Natural Numbers

A subset A 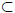R is an inductive set if it satisfies the following two properties :
i. 1 ∈ A
ii. If n ∈ A, then n + 1 ∈ A.

• R is an inductive set.
The set of natural numbers, N = {1, 2, 3, . . .}, is defined to be the intersection of all inductive
subsets of R.

• N is itself and inductive set and is contained in every other inductive subset of R. Why?
[The modern convention is to include 0 in the definition of an inductive set and therefore to define
the natural numbers as {0, 1, 2, . . .} . For our purposes, it is be more convenient to let N represent
only the positive natural numbers. However, when applying the principle and mathematical induction
or rescursive definitions (see below), it will be sometimes be convenient to start with 0 and so
implicitely include 0 in the inductive set.]

• If n ∈ N\{1} , then n − 1 ∈ N.
٠ Suppose n ∈ N but n ≠ 1. Therefore, by the definition of an inductive set, n = m + 1 for
some m ∈ N. Therefore, n −1 = m ∈ N.

Principle of Mathematical Induction

One immediate implication of this definition of the natural numbers is the principle of mathematical
induction. Suppose we are given a list of statements 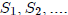and we wish to prove that all of them
are true. The principle of mathematical induction states that it is sufficient to prove the following
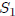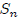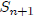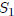two statements: (i) , and (ii) "For any natural number n, implies ." (Statement is
called the basis statement, 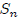is called the induction hypothesis, and the statement 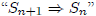is
called the induction step .) Once statements (i) and (ii) are established, we can prove any statement
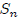by starting with stateme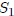nt and successively applying the induction step. A formal statement
and proof follows.

• Suppose we assign a logical statement 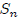to each n ∈ N, and suppose
(i) 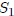is true, and (ii) 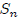implies .
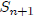Then 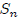is true for all n ∈ N.
٠ Let A = {n ∈ N : S(n) is true}. By assumption 1 ∈ A. Also if n ∈ A, then n + 1 ∈ A.
Therefore, A is an inductive set. But since N is contained in any inductive set, we have
N 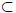A 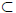N, which implies A = N.

Properties of Natural Numbers

We may use mathematical induction to establish that all natural numbers are positive and that
the set of natural numbers are discrete in the sense that if n ∈ N, then there is no m ∈ N such that
n < m < n + 1.

• (L1) n ∈ N implies n ≥ 1.
٠ The proof is by induction on n. First observe that 1 ≥ 1 provides the basis statement for
n = 1. Now consider the induction hypothesis n ≥ 1. Then, since the order axioms imply
n +1 > n, we have n + 1 > n ≥ 1, which establises the induction step.

• (L2)If m, n ∈ N and m > n, then m ≥ n + 1.
٠ If m > 1, then m −1 ∈ N and therefore the previous proposition implies m −1 ≥ 1. Therefore
m ≥ 1+1, which establishes the basis statement. Now suppose that m > n implies m ≥ n+1.
Then m > n+1 implies m−1 > n, which implies m−1 ≥ n+1 and therefore, m ≥ (n + 1)+1.

Using induction, we may also show that the natural numbers are closed under addition and multiplication .

• Suppose m, n ∈ N. Then (i) m + n ∈ N, and (ii) m ٠ n ∈ N. (iii) If m < n, then n − m ∈ N.
٠ (i) The proof is by induction. Consider any m ∈ N. Then, since N is inductive, we have
m+1 ∈ N. Now suppose m+n ∈ N. Then, since N is inductive, (m + n)+1 = m+(n + 1) ∈ N.
٠ (ii) The proof is by induction. Consider any m ∈ N. From the field axioms, we have m ٠1 =
m ∈ N. Now suppose m ٠ n ∈ N. Then m ٠ (n + 1) = m ٠ n + m ٠ 1 ∈ N by part (i).
٠ (iii) The proof is by induction on n. If m − 1 > 0, then since m ≠ 1, it follows that m = p+1
for some p ∈ N. But then m −1 = p ∈ N. Suppose m − n > 0 implies that m − n ∈ N. Then
if m − (n +1) > 0, then (m − 1) − n > 0 and m − 1 ∈ N implies m − (n +1) ∈ N.

Well Ordering Principle

If min B exists for each nonempty subset B 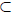X, then we say that a set X is well-ordered by '≤'.

• R is not well ordered by '≥'. Neither are the set of integers or the set of rationals defined below.

For any n ∈ N, the set 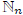≡ {m ∈ N : m ≤ n} is called the n^th-segment of N.

• N is well-ordered.
٠ Let A = {n ∈ N : if B 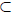N and 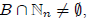then min B exists}. We will prove by induction
that A = N. From (L1), we have that 1 ≤ n for all n ∈ N. Therefore, if 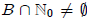, then
1 =minB. Therefore, 1 ∈ A, which is our basis statement.
٠ Now suppose n ∈ A. To show that n + 1 ∈ A, consider any B 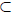N such that B ∩ ≠ '.
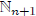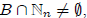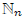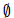Then either in which case min B exists by the induction hypothesis, or B ∩ = in which case m ∈ B implies n < m and therefore (L2) implies that n + 1 ≤ m. But then
B ∩ 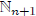≠ 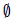implies min B = n + 1. Therefore n +1 ∈ A.
٠ To complete the proof, consider any nonempty subset B 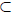N. Then n ∈ B implies B ∩ ≠ .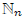
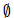But since n ∈ A, it follows that min B exists.

Principle of Recursive Definition.

When proving theorems is often useful to construction a sequence of elements (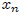) inductively
in which the value of each 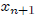is based on the values already defined for 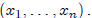Stated
equivalently in the langange of functions, for some set of possible values Y, we wish to construct
a function x : N → Y in which for each n ∈ N, the value of x(n + 1) depends on the value of the
restriction 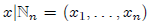that has already been defined. The following theorem provides a
formal statement of the requirements for constructing a unique sequence.

• (PRC): Suppose Y is a nonempty set and we are given a function σ : 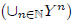→ Y. Then for
any a ∈ Y, there is a unique function f : N → Y for which (i) f(1) = a, and (ii) for each n ∈ N,
f (n + 1) = σ(f |).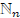
٠ (sketch of proof) We use mathematical induction to construct a unique sequence of functions
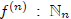→ Y and show that 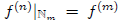for m < n. Then define
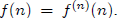
Complete proofs can be found in Royden, RealAnalysis and Kelly , General Topology.

Example: An example from decision theory illustrates an application of a recursive definition.
Suppose time is discrete and each point in time is represented by a positive integer. At each
point in time, the decision maker must choose some action in a set Y (e.g. Y = {Lef t, Right}).
An n-period history is an n-tuple 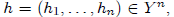where each ht specifies the decision
taken in period t. We let 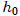denote the initial history in which no decisions have been made.
Then 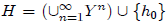denotes the set all (partial) histories. A strategy (or decision
rule ) is a function σ : H → Y, which specifies for each history h a choice in Y. An outcome is
a sequence 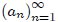that specifies the decision taken in each period n. Then the principle of
recursive definition implies that each strategy implies a unique outcome 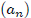, where
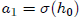
and 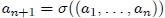for each period n ∈ N.

Monomials

In applying the principle of recursive definition, we often require a weaker version in which f (n+1)
depends only on f (n), rather than all of the information contained in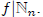. In this case we can
replace the function σ : 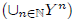→ Y with the simpler function s : Y → Y.

• (Principle of Simple Recursive Definition): Suppose Y is a nonempty set and we are given
a function s : Y → Y. Then for any a ∈ Y, there is a unique function f : N → Y for which (i)
f(1) = a, and (ii) for each n ∈ N, f (n +1) = s(f (n)).

We may use this simplified principle to define a monomial function .

For any x ∈ R, we define 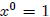. For any n ∈ N and x ∈ R, we define 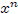≡ f (n) recursively as
follows

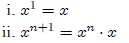
[The formal application of the simple PRD works as follows: Y ≡ R, a ≡ x, s(z) ≡ x ٠ z. Then
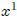≡ f(1) = x, and 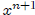≡ f (n + 1) = s(f (n)) = x ٠ f (n) ≡ x ٠ .]

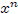• (a)
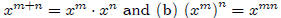
٠ The proof of (a) is by induction on n. By definition,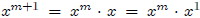 for any
m ∈ N. Suppose 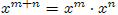for any m ∈ N. Then

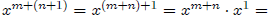
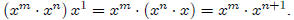
٠ The proof of (b) is by induction on n. Observe first that 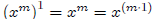for all m ∈ N.
Suppose 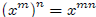for any m ∈ N. Then
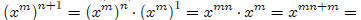
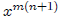,where the first and third equalities follow from part (a).