Period 1 Activity Sheet Solutions

1.1 What Are Ratios? How Are They Used?

Your instructor will introduce the concepts of ratios and “per.” Use this information to
answer the questions in this section.

a) Ratios are useful when making comparisons. Use ratios to compare the number
of miles each vehicle can travel using one gallon of gas.

1) A sports car uses 0.8 gallons of gas to travel 17
miles. How many miles per gallon does it get?

2) A sports utility vehicle uses 3.9 gallons to gas to travel
57 miles. How many miles per gallon does it get?

3) How many gallons of gas does the sports car require to travel 243 miles?

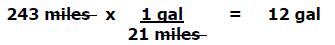
b) The next activity illustrates how ratios are used to convert units .

1) Using the blue balances on your table, place washers in the center of
one balance pan and plastic chips in the center of the other pan.
a) How many chips are required to balance one washer? __9__
b) Write the number of chips per washer as a ratio. _9 chips/1 washer _

2) Using the balance, find how many chips are required to balance one
metal nut. Write the number of chips per nut as a ratio.
_3 chips/1 nut_

3) Without using the balance, calculate how many nuts there are per washer.
Show the steps in your calculation , including units and how they cancel.

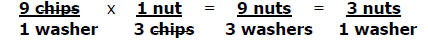
_3 nuts/washer_

4) Use the balance to check your answer to part c. How many nuts balance one
washer? _3_

c) Use ratios to convert 10 miles/1 gallon of gas into kilometers/liter. Show the
steps in the calculation, including units and how they cancel. (Hint: 1 mile =
1.609 kilometers and 1 gallon = 3.785 liters.)

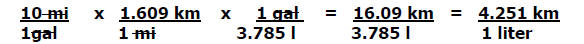
d) Group Discussion Question: List some common ratios . Why are ratios useful?

1.2 How are Ratios Used to Calculate Efficiency?

Your instructor will discuss ratios and the efficiency of energy processes.

a) Connect one hand-cranked generator to a second hand-cranked generator. Turn
the crank of the first generator slowly 10 full revolutions.

1) How many revolutions did the crank of the second generator turn?
___________

2) Calculate the efficiency of the system of two generators when the first
generator crank is turned slowly.

If the second generator crank turned 6.5 revolutions, the efficiency
= 6.5/10 = 0.65 = 65%

3) Turn the first generator’s crank rapidly 10 full revolutions. How many
revolutions did the crank of the second generator turn? _________ Calculate
the efficiency when the first generator crank is turned rapidly.

The efficiency will be greater when the crank is turned rapidly
because the effect of friction in the moving parts of the generator is
less.

4) Why does the efficiency depend on the speed of the cranking? Is it possible
to turn the first generator crank 10 revolutions so rapidly that the second
crank also turns 10 revolutions? Why or why not?

Turning the crank more rapidly reduces the friction in the gears of
the crank. However, it is not possible to turn the first crank so fast
that friction is eliminated . The system of two cranks is never 100%
efficient.

b) Watch the demonstration of an exercise bicycle connected to light bulbs. The
energy used to pedal the bicycle and to light the bulbs is measured in units of
joules.

1) Each lit bulb requires 50 joules of energy per second. What is the total
energy per second required to light all of the bulbs in this demonstration?
_250 J/s _

2) If the person pedaling the bicycle expends 1,300 joules of energy per
second, what is the efficiency of the bicycle and light system when all the
bulbs are lit?

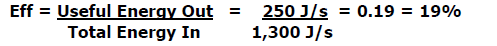
1.3 How Do Exponents and Scientific Notation Simplify Calculations ?

Your instructor will discuss the meaning of exponents. Use this information to calculate
the base 2 raised to an exponential power.

a) Bill says that 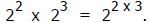Denise says that 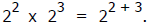To decide
whose method is correct , answer the questions below.

1) How much is

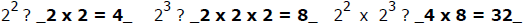
2) How much is

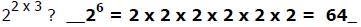
3) How much is

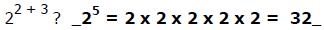
4) Based on your calculations, which method is correct? State the rule for
multiplying numbers with exponents.

Adding exponents gives the correct answer. When multiplying
numbers with exponents, add the exponents.

5) Apply the rule you found for the base 2 to calculations using the base 10
raised to an exponential power.

How much is

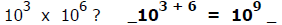
b) Sarah says that Jason says that
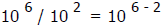
Based on your answer to question 4, predict the rule for dividing numbers with
exponents. Then check your rule by using it to answer the questions below.

1) How much is

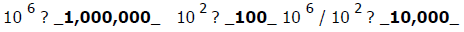
2) How much is

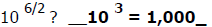
3) How much is

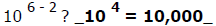
4) State the rule for dividing numbers with exponents.
When dividing numbers with exponents, subtract the exponents .

At this point, your instructor will give you information about scientific notation. Scientific
notation usually means writing one digit to the left of the decimal times the base 10
raised to an exponential power. For example, in scientific notation 13,300 = 1.33 x 10⁴.

c) Write each of the quantities below in scientific notation, as an integer, and in
words. First find the answer without using a calculator. Then check your
answer with a calculator.

Example: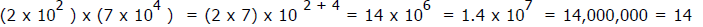 million

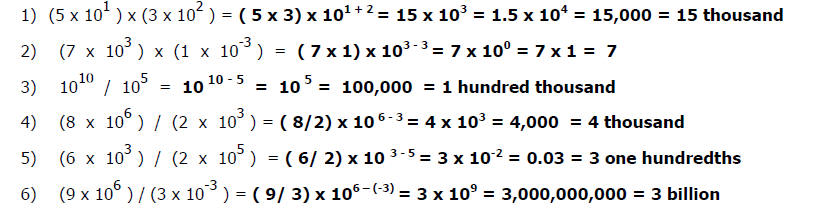
d) Your instructor will discuss the energy content of some common fuels. Use this
information, along with ratios and scientific notation, to make the comparisons
below.

1) How many kilograms of wood are needed to produce the same amount of
energy as 1 kg of coal?

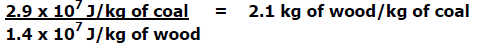
2) How many kilograms of crude oil are needed to produce the same amount of
energy as 1 kg of Uranium ²³⁵?

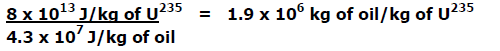
3) An electric generating plant burns coal to produce electricity. If burning 1 kg
of coal produces 1.1 x 10⁷ joules of energy, what is the efficiency of burning
coal to produce electricity?

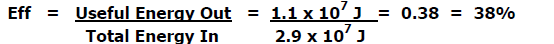
1.4 What is the Difference between Linear and Exponential Growth?

Your instructor will discuss linear and exponential growth using the graph on the next page.

Fig. 1 Sample Data on Energy Use and Population

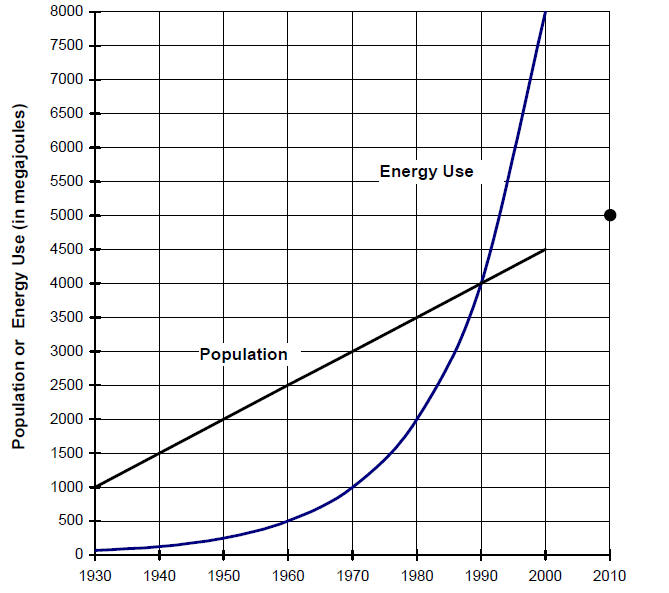
a) Find the rate of increase (the slope) of the linear graph. _50 people/yr _

b) If this growth rate remains constant after the year 2000, what will the population be
in 2010? _5,000_ Add a data point to the graph to show the population in 2010.

c) Starting with 1970, find the doubling time of the exponential graph. _10 years_

d) If energy use continues to increase at the same rate, what will the energy use be in
2010? _16,000 MJ _ Where would a data point for energy use in 2010 be located?
Above the top of the page.

e) Using the doubling time from part c), calculate the energy use in 1930. _62.5 MJ_

f) Group Discussion Question: If someone gave you $1 and offered to double every
day the amount you have, how much would you have on day 7? _$1 x 2⁶ = $64__
How much would you have on day 30? _$1 x 2²⁹ = $ 536,870,912__