Polynomial Codes and some lore about Polynomials

10.3 Which Polynomials Make Good Codes?

The polynomials we want are those that are not only prime, but primitive as well.
A primitive polynomial is one for which every possible remainder is a remainder of
some power of x .

Why primitive polynomials?

The degree of an encoding polynomial counts the number of check bits in its
code. A single bit error, produces an unknown monomial “error polynomial” which gets
added to our message , whose remainder will be a remainder of a power of x. The number
of bits we can handle in our code is the number of different monomial remainders , which
is the number of remainders of powers of x. Thus, for efficiency in constructing single bit
error correcting codes, we want to have as many possible remainders that are remainders
of powers of x This number is maximized for a given degree of a polynomial, by
definition, by a primitive polynomial.

Consider the simplest non -trivial example, which is the polynomial 1+x+x³.

What are possible remainders?

Because our polynomial has degree 3, a remainder is a polynomial of the form
a+bx+cx²; that is, a polynomial of degree one less than that of our polynomial, such
that a b and c are each chosen from (0,1), and not all are 0. (If x^k were to have 0
remainder that means our polynomial is a factor of a monomial so it would have to be a
monomial, and that is too silly for us to consider)

If our polynomial has degree k, the number of such possible remainders is 2^k-1,
which for k=3 is 7. The possible remainders are 1,x,x², 1+x, 1+x², 1+x+x². and x+x².

It is slightly more convenient to represent these remainders as 3 (or more generally k)
component vectors, in which form we would write them as 100, 010, 001, 110, 101, 111, and
011.

Sometimes, when you want to recognize them easily you can interpret them as
numbers. The way I like to do it is perhaps not the best but it works. I treat them as binary
numbers read backwards; they then read 1,2,4,3,5,7, and 6 in the order given.

Our polynomial will be primitive if every one of these remainders is the
remainder of some power of x. We can test for this by writing out the remainders of
powers in ascending order. We know that x⁰ =1 has remainder 1.

We will be able to write out the remainders of all powers if we give a rule for
finding the remainder of x^j+1 given the remainder of x^j.

We will be able to apply this rule on a spreadsheet by entering the rule on one
row, and then copying it down, so we will be able to investigate whether a polynomial is
primitive or not very quickly on a spreadsheet.

So what is the rule for finding the remainder of x^j+1 from that for x^j?

Suppose we have Remainder of .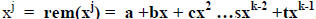

We get x^j+1 from x^j by multiplying it by x. We know that x^j = p(x)q(x) + rem(x^j) for some
q(x)..

We therefore have x^j+1 = p(x) [xq(x)] + xrem(x^j), the first term of which has no remainder
so we have rem(x^j+1) = rem(xrem(x^j)).

If the coefficient, t, of x^k-1, is 0, the effect of multiplying rem(x^j) by x is to increase each
power by 1, so that we would have rem(x^j+1) = ax + bx² + cx³ … if t=0.

If instead t=1, the last term in rem (x^j), when multiplied by x becomes x^k whose remainder
is (p(x)-x^k).

We conclude, that the general form for the remainder of x^j+1 here is

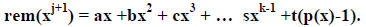
Suppose we consider the polynomial p given by p(x) = x³ + x + 1. Its remainder
has three coefficients and let us denote them as a b and c as above.

The rule for going from x^j to x^j+1 in is then (a,b,c) becomes (c, a+c, b). The a and
b terms move over 1 place to the right and c goes to the 1 + x places.

The remainders of powers, according to this rule are

Power		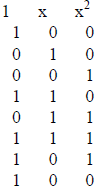binary number

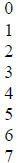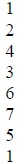We call this a remainder table for the polynomial p(x).

You will notice that every remainder appears on this list, which means that the
first time 1 appears as a remainder for the second time is at the 7^th power, more generally
for a primitive power the remainder of 1 first happens at the (2^k-1)^st power. This is the
behavior of a primitive polynomial.

Notice that the matrix appearing in the middle of the chart up to the 7^th row which
is the power 6 row here is essentially a Z type matrix with an identity matrix on top. Thus
iif we start at the power 3 row and take 7 rows in order starting there, we get our old
friend, the message destroyer, D.

How can we test a polynomial for primitivity?

We can set up a spreadsheet to generate the remainders of powers, and locate the
first power for which the binary number is 1. If that power is 2^k -1 we have a primitive
polynomial, and otherwise not.

Once you have set up a test spreadsheet this way, you can change the polynomial
to be tested by changing the line on which you enter its succession rule, and copy it down
to apply it everywhere. This involves modifying at most k-1 entries and copying.
(the a entry is always t so it never changes.)

You can test polynomials for primitivity without a spreadsheet by using tricks.
Thus the remainder of x^2j is the square of the remainder of x^j. If you only write the
remainders of the even powers from k to 2k-2, you can compute all the remainders of
powers of the form 2^j from these, and if you find that the remainder of the 2^k th power is
not x, you know that the polynomial is not primitive. It can happen that the remainder of
2^k is x and the code is not primitive, if the remainder of some lower power is also x. You
can check this by checking whether the remainders powers that are factors of 2^k-1 are 1.
If not the polynomial is primitive.

In our example, we have rem(x⁴) = x+x²

Squaring we get rem(x⁸) = rem (x² + x⁴) = x, and our code is a candidate for primitivity.
Since 2^k – 1 is a prime, this implies that the polynomial is primitive.

Why is primitivity important to us?

Our plan for decoding is to divide the received message, r(x), by the encoding
polynomial, p(x), and examine its remainder, rem(r(x)). Since the encoded message,
m(x)p(x), has no remainder, performing this division to find the remainder will be our
message killer. This remainder comes entirely from errors and it contains the information
we need to find the error.

Suppose the error is in the bit corresponding to the monomial x^e.

We can find the error location, (called e here,) by finding the power of x that
has remainder given by our observed rem(r(x)), something that can be read off from
the remainder table.

Primitive polynomials have the largest number of distinct rows in their remainder
tables for their degrees as is possible since every polynomial of degree less than that of
the primitive polynomial is the remainder of some power of x.

Notice that once there is a repetition in the remainder table, the table cycles. The
remainder of the next power depends only on the remainder of the present one . Therefore,
if the remainder of x^a is the same as that of x^b, this will be true of x^a+s and x^b+s for all s.