Quadratic Equations Worksheet
1. Factor into at least two factors:
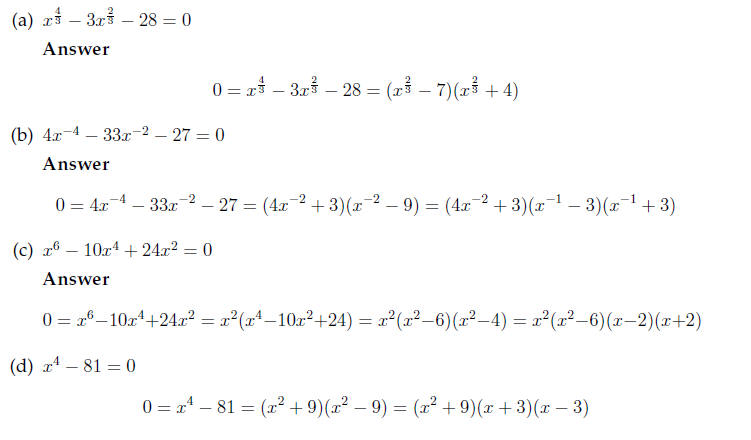
Answer
2. Find all real solutions of the following equations:
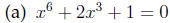
Answer The reduced quadratic equation is t^2+2t+1 = 0 with t = x^3.
Factoring
we obtain t^2+2t+1 = (t+1)^2 = 0 and whence the set of solutions to the reduced
quadratic equation is {−1}. Solving t = x^3 = −1 we obtain {−1} as the set of
solutions to the original equation. [Note that since t = −1 is a root of degree
2
of the reduced quadratic , x = −1 is a root of degree 2 of the original
equation.]
Another way to solve this problem is to observe that x^6+2x^3+1 = (x^3+1)^2 = 0
and therefore the solutions satisfy x^3 = −1, which produces the solution set
{−1}.
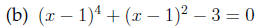
Answer The reduced quadratic is t^2 + t − 3 = 0 with t = (x − 1)^2. By
the
quadratic formula we have
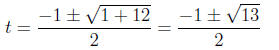
The solution set of the reduced quadratic is therefore
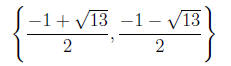
and to obtain the solution set to the original equation we solve
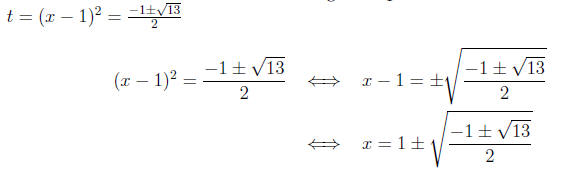
Observe that since
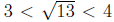the above calculation produces two complex
solutions. The solution set of the original equation is therefore
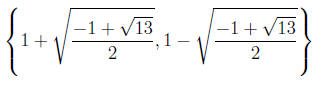
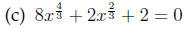
Answer The reduced quadratic equation is 8t^2 + 2t + 2 = 0 with
.
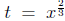Computing the discriminant shows that since it is 4 − 4(8)(2) < 0 that the
reduced quadratic has no real solutions and therefore the original equation
does not have any real solutions. The solution set is therefore the empty set,
.
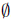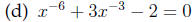
Answer The reduced quadratic equation is
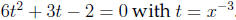
By the quadratic formula we obtain
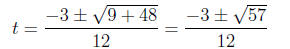
The solution set of the reduced quadratic equation is therefore
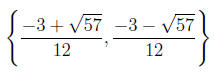
We need to solve t = x−3 for each element of this solution set in order to
obtain
the solutions to the original equation.
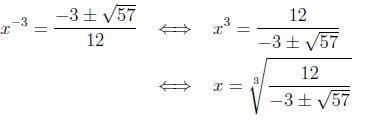
The solution set of the original equation is therefore
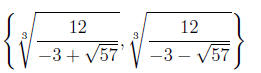
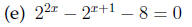
Answer The reduced quadratic equation is t^2 − 2t − 8 = 0 with t = 2x, which
factors as (t − 4)(t + 2) = 0. This tells us that the original equation factors
as
(2x − 4)(2x + 2) = 0 and either 2x = 4 -> x = 2 or 2x = −2, which is impossible.
The solution set of the original equation is therefore {2}.
| Prev | Next |