Rational Expressions

When you want to add or subtract fractions, you need a common denominator.
Of course, it makes life easier if you have the least common
denominator of the expression. However, it is not completely necessary to
find the least commond denominator because you can simplify the expression
after you perform the operation. It just may be easier to find the least
common denominator at the beginning so you do not have to worry about
simplifying a complicated expression at the end. For example, say we want
to subtract

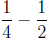
We can see that 4 = 2 · 2, so the least common denominator is 4. Then, we
can solve this :

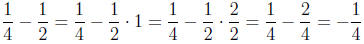
However, we can add general fractions by forcing the denominators to be
common denominators (which may not be the least common denominator).
This is accomplished by multiplying both terms by 1, except we use a specific
way of writing it. We multiply by 1 as 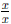where x is the denominator of the
other term:

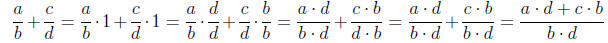
Sometimes this is called "cross multiplying" because we end up with a numerator
of the sum of the terms you would get if you made an X between the
fractions and multiplied the terms opposite each other, and the denominator
is the product of the denominators :

What we have here is ad from the \ part of the X, and bc from the / part of
the X. Then, the denominator is the product of the old denominators.

We can easily write any subtraction as an addition problem as:

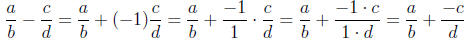
So, we now know how to add, subtract, multiply and divide fractions .

Thankfully, rational expressions are nothing other than fractions. The
bad thing is that we do not know the numbers that are the numerator and
denominator because they depend on some variable. However, all we have to
worry about is not dividing by zero. For this reason, we have to make sure
that we take note of the x values that will make the denominator of any of
the terms in the original expression zero. Then, we say the expression is not
defined for these x values by specifying our domain, as stated earlier. If you
know how to add, subtract, multiply and divide fractions, you know how to
add, subtract, multiply and divide rational expressions.

However, the problem comes in when we are faced with the task of reducing
the fraction. It is a good idea to factor the original expressions
completely before trying to perform any operations. When multiplying (and
dividing, since it is essentially a multiplication), it is a good idea not to multiply
the terms out. After an addition or subtraction, it is a good idea to try
to factor again . Doing these makes it easier to:

• find the domain of the expression

• find the least common denominator of an expression

• simplify the expression by cancelling terms

Now that we have an idea of how to attack these problems, let's do some
examples.

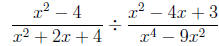
First, we factor all of the expressions:

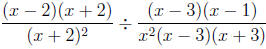
Now, we need to figure out the domain. From the first term, we know we
can not have x + 2 = 0 i.e. x ≠ -2. In the second term, we can not have
a denominator of zero, so x ≠ 0, x ≠ 3 and x ≠ -3. Finally, since we are
dividing by the entire second term, it can not equal zero. Therefore, the
numerator of the second term can not be zero either. This happens when
x = 3 or x = 1. Putting it all together, our domain is { x ∈ R such that
x ≠ -3 and x ≠ -2 and x ≠ 0 and x ≠ 1 and x ≠ 3}. Next, we simplify:

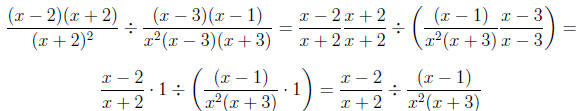
We still have not done anything except find the domain and simplify. Now,
we can " flip the second and multiply."

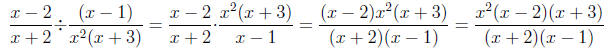
At this point, we try to simplify. However, there are no common factors in
the numerator and denominator, so we can not do anything else. We can
either leave this as it is, or multiply it out. We will leave this as it is.

Now, consider a more complicated example.

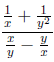
This problem incorporates all of the operations of fractions . However, there
is not much we can do to this. Order of operations tells us to do parenthases
then exponents . Niether of those appear in this equation. Then, we are supposed
to multiply and divide next. However, we do not know the reciprocal
of the entire denominator. Therefore, we have to simplify it. We can work
with the numerator and the denominator and try to make each of them one
fraction by performing the addition or subtraction:

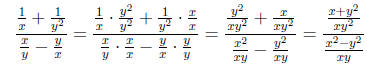
Since we have not cancelled any terms, we have not changed the domain
yet. So, we will get the domain from this expression. We know that xy²
can not equal zero, and xy can not equal zero. Finally, since the entire big
denominator can not be zero, x² -y² can not equal zero. We know from the
first two conditions that x ≠ 0 and y ≠ 0. Now, lets find when x² - y² = 0.
This happens when x² = y², or when x = ± y (because (-a)² = a² for all
real numbers a). Therefore, our domain is { x ∈ R such that x ≠ 0, y ≠ 0
and x ≠± y}.

The expression can now be rewritten as

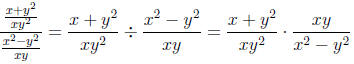
Now, we can factor and then multiply:

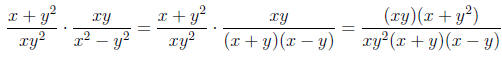
Now, we can simplify this by canceling xy:

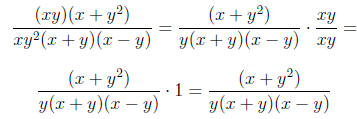
At this point, there is no further simplification possible. We can not factor
the numerator any more, so we will not be able to cancel with any of the
terms in the denominator.