Reducing Rational Functions

The goal of this section is to learn how to reduce a rational expression to “lowest terms.”
Of course, that means that we will have to understand what is meant by the phrase
“lowest terms.” With that thought in mind, we begin with a discussion of the greatest
common divisor of a pair of integers.

First, we define what we mean by “divisibility.”

Let’s look at an example.

Example 2. What are the divisors of 12?

Because 12 = 1×12, both 1 and 12 are divisors of 12. Because 12 = 2×6, both 2
and 6 are divisors of 12. Finally, because 12 = 3 × 4, both 3 and 4 are divisors of 12.
If we list them in ascending order , the divisors of 12 are

1, 2, 3, 4, 6, and 12.

Let’s look at another example.

Example 3. What are the divisors of 18?

Because 18 = 1 × 18, both 1 and 18 are divisors of 18. Similarly, 18 = 2 × 9 and
18 = 3 × 6, so in ascending order, the divisors of 18 are

1, 2, 3, 6, 9, and 18.

The greatest common divisor of two or more integers is the largest divisor the
integers share in common. An example should make this clear.

Example 4. What is the greatest common divisor of 12 and 18?

In Example 2 and Example 3, we saw the following.

Divisors of 12 :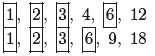
Divisors of 18 :

We’ve framed the divisors that 12 and 18 have in common. They are 1, 2, 3, and 6. The
“greatest” of these “common” divisors is 6. Hence, we say that “the greatest common
divisor of 12 and 18 is 6.”

Thus, as we saw in Example 4, GCD(12, 18) = 6.

When the greatest common divisor of a pair of integers is one, we give that pair a
special name.

For example:

• 9 and 12 are not relatively prime because GCD(9, 12) = 3.
• 10 and 15 are not relatively prime because GCD(10, 15) = 5.
• 8 and 21 are relatively prime because GCD(8, 21) = 1.

We can now define what is meant when we say that a rational number is reduced
to lowest terms.

As we saw in Example 4, the greatest common divisor of 12 and 18 is 6. Therefore,
the fraction 12/18 is not reduced to lowest terms. However, we can reduce 12/18 to
lowest terms by dividing both numerator and denominator by their greatest common
divisor. That is,

Note that GCD(2, 3) = 1, so 2/3 is reduced to lowest terms.

When it is difficult to ascertain the greatest common divisor, we’ll find it more
efficient to proceed as follows:

• Prime factor both numerator and denominator.
• Cancel common factors.

Thus, to reduce 12/18 to lowest terms, first express both numerator and denominator
as a product of prime numbers, then cancel common primes.

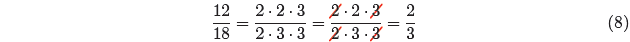
When you cancel a 2, you’re actually dividing both numerator and denominator by 2.
When you cancel a 3, you’re actually dividing both numerator and denominator by 3.
Note that doing both (dividing by 2 and then dividing by 3) is equivalent to dividing
both numerator and denominator by 6.

We will favor this latter technique, precisely because it is identical to the technique
we will use to reduce rational functions to lowest terms. However, this “cancellation”
technique has some pitfalls, so let’s take a moment to discuss some common cancellation
mistakes.

Cancellation

You can spark some pretty heated debate amongst mathematics educators by innocently
mentioning the word “cancellation.” There seem to be two diametrically opposed camps,
those who don’t mind when their students use the technique of cancellation, and on
the other side, those that refuse to even use the term “cancellation” in their classes.

Both sides of the argument have merit. As we showed in equation (8), we can
reduce 12/18 quite efficiently by simply canceling common factors. On the other hand,
instructors from the second camp prefer to use the phrase “factor out a 1” instead of
the phrase “cancel,” encouraging their students to reduce 12/18 as follows.

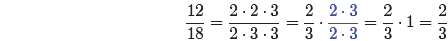
This is a perfectly valid technique and one that, quite honestly, avoids the quicksand
of “cancellation mistakes.” Instructors who grow weary of watching their students
“cancel” when they shouldn’t are quite likely to promote this latter technique.

However, if we can help our students avoid “cancellation mistakes,” we prefer to
allow our students to cancel common factors (as we did in equation (8)) when reducing
fractions such as 12/18 to lowest terms. So, with these thoughts in mind, let’s discuss
some of the most common cancellation mistakes.

Let’s begin with a most important piece of advice.

As a first example, consider the rational expression

which clearly equals 8/2, or 4. However, if you cancel in this situation, as in

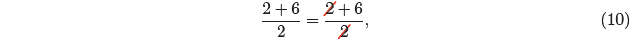
you certainly do not get the same result. So, what happened?

Note that in the numerator of equation (10), the 2 and the 6 are separated by a
plus sign . Thus, they are not factors; they are addends! You are not allowed to cancel
addends, only factors.

Suppose, for comparison , that the rational expression had been

which clearly equals 12/2, or 6. In this case, the 2 and the 6 in the numerator are
separated by a multiplication symbol , so they are factors and cancellation is allowed,
as in

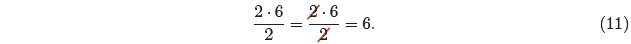
Now, before you dismiss these examples as trivial, consider the following examples
which are identical in structure. First, consider

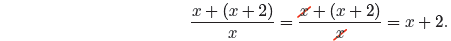
This cancellation is identical to that performed in equation (10) and is not allowed.
In the numerator, note that x and (x+2) are separated by an addition symbol , so they
are addends. You are not allowed to cancel addends!

Conversely, consider the following example.

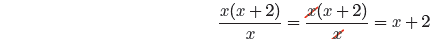
In the numerator of this example, x and (x+2) are separated by implied multiplication.
Hence, they are factors and cancellation is permissible.

Look again at equation (10), where the correct answer should have been 8/2, or 4.
We mistakenly found the answer to be 6, because we cancelled addends. A workaround
would be to first factor the numerator of equation (10), then cancel, as follows.

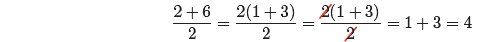
Note that we cancelled factors in this approach, which is permissible, and got the
correct answer 4.