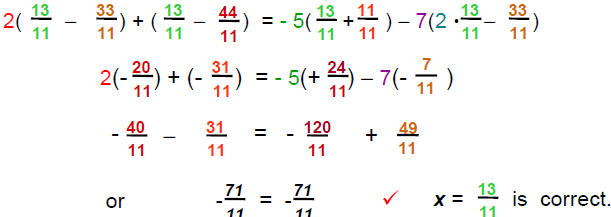Solving Linear Equations

In this section we will combine all of the methods that we have learned to solve any
linear equation containing fractions, decimals, and parentheses. We will use all of
properties that we learned in Chapter 1 to simplify the expressions on both sides of the
equation.

DEFINITION A simple linear equation in one variable is any equation that can be
put in the form of ax + b = 0, where a and b are real numbers, a ≠ 0.

The alternate form of this equation is : A x = B or A = B x

Extend this to the general form of the equation.

General equation: Ax + B = C x + D (A, B, C, D are real numbers.).

i) Simplify the equation so that there are only integers on both sides
ii) Many equations have enclosures which must first be simplified.
iii) Then solve simplified equations vertically - using the balance beam.

Pattern: a x + b = c x + d Both sides simplified (a ,b, c, d are integers.)
Look at the coefficients of x and determine which is the larger integer (furthest to
the right on the number line ). If c > a then we will keep the variable x on that side of
the equation and keep the constant on the other side. To do this we first add
opposites on the balance beam below the equation. Look at the pattern, and then
follow the same steps through several examples
Solve simplified equations vertically - using the balance beam .

Equation: a x + b = c x + d Both sides simplified (a ,b, c, d are integers.)

Pattern: c > a

1) Add opps :

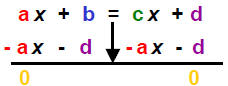
Complete the step:

	Let A = (c- a) and B = (b - d)
Then: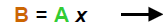	A > 1 is coefficient of x

2) Multiply recip:

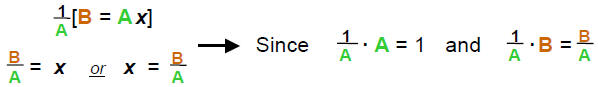
Example 1: Solve 3(x − 2) = 5

Procedure: 3(x − 2) = 5

1) Remove parentheses :	3x − 6 = 5
2) Add opps: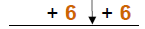
Complete the step:		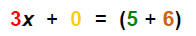Note: (5 + 6) = 11
Then		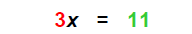3 is the coefficient of x
3) Multiply recip:		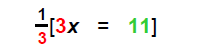Since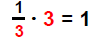
Then		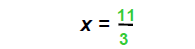and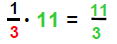
4) Check in original equation:	3(x − 2) = 5
Replace in the equation:
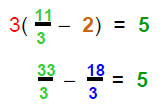or	5 = 5	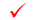x = is correct.

Solving Linear Equations

Simplify equations that contain decimal fractions first by multiplying by the LCD.
Example 2:

Solve	0.05x + 0.07(100 − x) = 6.2
Procedure:	0.05x + 0.07(100 − x) = 6.2
Multiply LCD :	100[0.05x + 0.07(100 − x) = 6.2 ]
	5x + 7(100 − x) = 620	Distributive Property
Remove parentheses :	5x + 700 − 7x = 620
Collect like terms :	-2x + 700 = 620	Commutative Property

Simplify using balance beam:

1) Add opps:		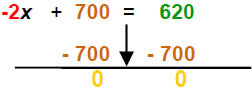Add same thing to both sides
Complete the step:	-2x = - 80	(620 − 700) = - 80
2) Multiply recip:	-1/2[ 2x = 80 ]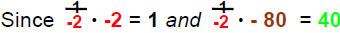
Then	x = 40
3) Check in original equation:	0.05x + 0.07(100 − x) = 6.2
Replace x	0.05(40) + 0.07[100 − (40)] = 6.2
Simplify:	2 + 7 − 2.8 = 6.2
or	- 1 = - 1 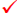x = 6.2 is correct.

Make special note of this example –

This is the type of equation that will be found in applications involving rates, percents
and investments.

Example 3:

Solve	2(x − 3) + (x − 4) = − 5 (x +1) − 7(2x – 3)
Procedure:	2(x − 3) + (x − 4) = - 5(x +1) − 7(2x – 3)
Remove parentheses:	2x − 6 + x − 4 = - 5x − 5 − 14x+ 21	Distributive Property
Collect like terms:	3x − 10 = -19x + 16	Commutative Property
Simplify using balance beam:
1) Add opps:		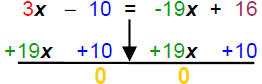Note that 3 > -19 Add same thing to both sides
Complete the step:	(3 + 19)x = +10	(3 + 19) = 22 and (16+10) = 26
Then	22x = 26	22 is the coefficient of x
2) Multiply recip: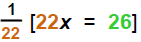
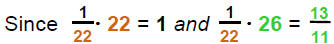Then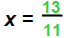
3) Check in original equation:	2(x − 3) + (x − 4) = - 5(x +1) − 7(2x – 3)
Replace x

Example 4:

Solve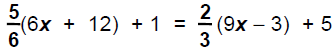

Procedure: 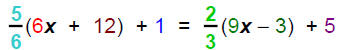Distributive Property
1) Remove parentheses: ·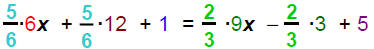

Complete the step: 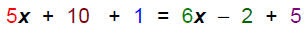Associative Property

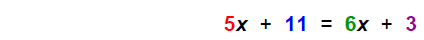
==>Solve vertically: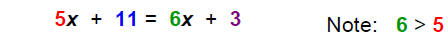

2) Add 0pps: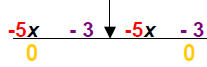

Complete the step: 8 = x or x = 8

3) Check: