Some Problems from Arithmetika
II.10. Find two square numbers whose difference is a given number, say 60.
If we call one of the unknown squares x2, then
Diophantus’s idea is to name the other one
as a variation on that one – by calling it (x + 5)2. Then the condition of the
problem is that
(x + 5)2 − x2 = 60, 10x + 25 = 60. Thus the problem has been reduced to a linear
equation, which
can be solved by simplifying and working in reverse: 10x = 35, x =35/10=7/2and x + 5 =17/2 .
Diophantus was almost always satisfied with finding one solution of a problem ,
although he
sometimes stated general properties . We can look more closely at this solution
technique and find
more solutions which would have been acceptable to Diophantus. Instead of x2 and
(x + 5)2, let
the two squares be x2 and (x + a)2. The second degree terms still cancel out,
and we are again left
with a first degree equation , 2ax+a2 = 60. If a2 is too large, then the solution
is negative. So what
we see is that if a is any integer such that 1 ≤ a ≤ 7 then
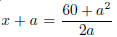 and
and
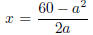 are
are
two positive rational numbers whose squares differ by 60. (Taking a = 6 leads to
82 and 22 as two
integral squares whose difference is 60, but Diophantus was satisfied with a
more complicated pair.)
Questions: If 60 is replaced by another positive integer, does the procedure
succeed in solving
the new problem? (That is, is every positive integer the difference of two
squares – of rational
numbers?) Can we find two cubes whose difference is a given number, say 60,
either by this method
or some other procedure? (Is every positive integer the difference of two cubes
– of rational numbers ?)
A Closer Look at Diophantus’s solution of II.8.
A square a2 is given, where a is any positive integer. For illustration
purposes, Diophantus
took a2 = 16. We wish to express this square as the sum of the squares of two
rational numbers.
Split it as follows: a2 = x2 + (a2 − x2), where x is to be determined. We want
a2 − x2 to be a
square, so [here is Diophantus’s inspired idea] we will express it as the square
of a linear expression
involving x and we will choose the constant term in the expression so that the
a2 term is matched,
i.e., a2 − x2 = (mx − a)2. (We’ll see shortly why mx − a was chosen instead of
mx + a.) Squaring
out and simplifying leads us to a linear equation for x, which is the trick we
saw in the example
above:
a2 − x2 = m2x2 − 2amx + a2, 2amx = m2x2 + x2 = (m2 + 1)x2, 2am = (m2 + 1)x
since x = 0 isn’t considered to be a number. Thus
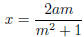 . So no matter what m is, as long as
. So no matter what m is, as long as
it is a positive rational number, this value of x will solve the problem for us.
If we use the special value m = 2, which was Diophantus’s choice (i.e., he
matched a2 −x2 with
(2x − a)2), we will obtain x = 4a/5, so that x2 = 16a2/25, a2 − x2 = 9a2/25. His
conclusion is that
every square is the sum of two squares , with the splitting
a2 = (3a/5)2 + (4a/5)2.
Notice the Pythagorean triple, 3,4,5! In hindsight, Diophantus could have told
his readers that since
32 +42 = 52, (3a)2 +(4a)2 = (5a)2, and so every a2 is the sum of the two squares
(3a/5)2 +(4a/5)2.
Generalizing and future results.
(a) If we match with a general (mx − a)2,
where m is any natural number, then 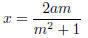
and a2−x2 turns out to be
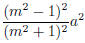 .The splitting is a2 = x2+y2 where
.The splitting is a2 = x2+y2 where
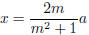 and y =
and y =
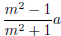 . If you remove the common factor a 2 from this relation and then multiply
the result by
. If you remove the common factor a 2 from this relation and then multiply
the result by
(m2 + 1)2, out pops this statement: (2m)2 + (m2 − 1)2 = (m2 + 1)2. So Diophantus
is really
rediscovering Plato’s Pythagorean triples!!
(b) Diophantus showed that every square is the sum of two squares. When Pierre
de Fermat
studied the Arithmetika he was fascinated by this fact and tried to extend it in
various directions.
He wrote that every cube is the sum of three cubes but not the sum of two cubes,
every fourth
power (bi-quadrate, in his terminology) is the sum of four fourth powers but not
the sum of two
fourth powers, etc. Part of this collection of statements is the famous
“Fermat’s Last Theorem,”
which was stated in the 17th century but not proved until the 1990’s.
| Prev | Next |