18.100B Problem Set 1 Solutions
1) The proof is by contradiction. Assume ∃r ∈ Q such that
r2 = 12. Then we may write r as
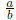
with a, b ∈ Z and we can assume that a and b have no common factors . Then
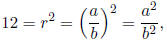
so 12b2 = a2.
Notice that 3 divides 12b2 and hence 3 divides a2. It follows that 3 has to
divide a (one way
to see this: every integer can be written as either 3n,3n+1,
or3n+2 for some integer n. If you
square these three choices, only the first one
gives you a multiple of three.)
Let a =3k, for k ∈ Z. Then substitution yields 12b2 = (3k)2 =9k2, so dividing by
3 we have
4b2 =3k2, so 3 divides 4b2 and hence 3 divides b2. Just as for a, this
implies that b has to divide
b. But then a and b share the common factor of 3, which contradicts our choice
of representation
of r. So there is no rational number whose square is 12.
2) S ⊆ R, S ≠ Ø, and u = sup S. Given any n ∈ N, ∀s ∈ S,
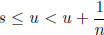, so 
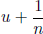is
an upper
bound for S. Assume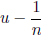 
is also an upper bound for S. Since
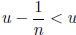, u would not
be the
least upper bound for S, which is a contradiction. Therefore
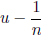is not an upper
bound for S.
3) Recall that a subset of the real numbers , A ⊆ R, is bounded if there are real
numbers a and a'
such that
t ∈ A ⇒ a' ≤ t ≤ a.
Since A, B ⊆ R are bounded, they have upper bounds a and b respectively, and
lower bounds a'
and b'. Let α = max (a, b) and β = min (a', b'). Clearly,
t ∈ A ⇒ β ≤ a' ≤ t ≤ a ≤ α
t ∈ B ⇒ β ≤ b' ≤ t ≤ b ≤ α,
hence any t ∈ A ∪ B satisfies β ≤ t ≤ α and A ∪ B is bounded.
Notice that, in particular, this shows that max{sup A, supB} is an upper bound
for A∪B, so
we only have to show that it is the least upper bound. Suppose γ< max{sup A, supB}. Then
without loss of generality, γ< supA. By definition of
supremum, γ is not an upper bound of A,
so ∃a ∈ A with γ<a. But a ∈ A ⇒ a ∈ A ∪
B, so γ is not an upper bound of A ∪ B. Therefore
max{sup A, supB} = supA ∪ B.
4) Start by noting that, if n, m ∈ N then
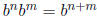from which it follows that
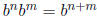for
n, m ∈ Z (why?). Similarly, you can show that
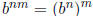for n, m
∈ Z. Recall that, if x> 0,
then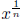 
is defined to be the unique positive real number such that
.
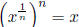a ) We have that m/n = p/q so mq = pn. Notice that
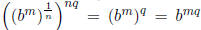and
that
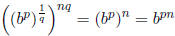, which is also equal to
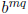. But we know that there is a
unique real
number y satisfying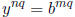 
hence the two numbers we
started with have to be equal, i.e.,
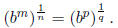
Notice that if this equality didn't hold, then we could not make sense of the
symbol b r for
r ∈ Q, because the value would change if we wrote the same number
r in two different ways.
b) Let r, s ∈ Q with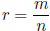 
and
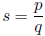. Since nq is an integer we know that
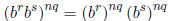
but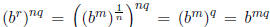 
and similarly
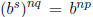. Since mq and np
are
integers we can conclude
.
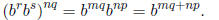
But there is a unique positive real number, y, such that
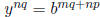, so we
know that
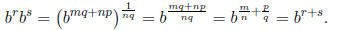
c) Now with b> 1, given r, s ∈ Q, s ≤ r we want to show bs ≤ br. Let
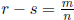,0
<n,0 ≤ m
since s ≤ r. Then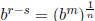 
, and it is easy to see that 1 ≤ bm, since 0 ≤ m
and 1 <b.
Thus a positive power of b r-s is greater than or equal to 1, which
implies 1 ≤ br-s. Multiplying
by bs gives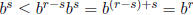 
, so bs ≤ br
. Hence for any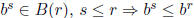 
,
so br is an upper bound for B(r).
Since br ∈ B(r), br must be the least upper bound, so
br = supB(r).
d) So let x, y ∈ R. If r, s ∈ Q are such that r ≤ x, s ≤ y, then r + s ≤ x + y so
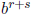∈ B(x + y)
and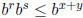 
. Keeping s fixed, notice that for any r ≤ x we
have
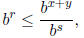
thus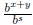 
is an upper bound for B (x) which implies
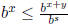. We rearrange
this to
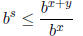
and conclude that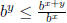 
or
.
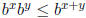Suppose the inequality is strict . Then ∃t ∈ Q, t<x + y, such that
.
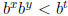We will find
r, s ∈ Q, with r ≤ x, s ≤ y and t<r+s<x+y. First, find N ∈ N so that
N (x + y - t) > 1,
then find r ∈ Q so that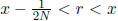 
and s ∈ Q such that
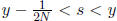(the existence
of N, r, s follow from the Archimedean property of R as shown in class). Now,
notice that
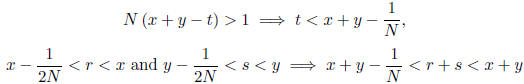
hence we have t<r + s<x + y just like we wanted .
But now we have
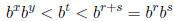
which is a contradiction because, since r<x and s<y, we
have br <bx and bs <by!
5) We know that in any ordered field , squares are greater than or equal to zero .
Since i2 = -1, this
means that 0 ≤-1. Butthen1=0+1 ≤-1+1=0 ≤ 1 which implies 0 =
1, a contradiction!
6) I'll write 
for this relation on C to distinguish it from the normal order on
R. To show that
is an order on C, we must show both transitivity and totality
(or given x, y ∈ C, exactly one of
the following is true: x 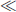y, y
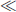x, or x = y).
First for transitivity, let x, y, z ∈ C, x = a + bi,
y = c + di, z = e + fi such
that x 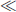y 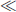z. Therefore a ≤ c ≤ e, so a ≤ e by the transitivity of
the order on R.
If a<e, then x 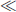z, so we are done. If a = e, then a = c = e so we have from
the
definition of 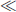that b<d<f, so once again by the transitivity of the order on R,
b<f.
Now a = e and b<f ⇒ x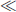 
z, so we have shown transitivity.
Now to show
totality. Consider x, y ∈ C, x = a + bi, y = c + di. Without loss of generality,
let a ≤ c. Suppose a = c. Then b<d ⇔ x
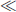y, b>d ⇔ y
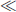x, and b = d ⇔ x = y, so by
the
totality of the order on R, we have the totality of
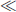on C in the case of a =
c. Suppose instead
that a<c. Then we know x 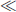y, and it is not the case that y
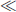x
or x = y, so we have totality
in this case as well. Thus we have proven that
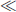is
an order on C.
This order does not have the least-upper-bound property. Consider
the set of complex numbers
with real part less than or equal to zero:
S = {a + bi : a ≤ 0,b ∈ R}.
S is bounded above, for instance by the number 1, but it is not possible for any
number z = a+bi
to be the supremum of S. If a ≤ 0, then a + bi
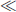a +(b + 1)i ∈ S,
so a + bi is not an upper
bound for S. If a> 0, then a +(b - 1)i 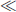a + bi, and a
+(b - 1)i is also an upper bound for S,
so a + bi is not the least upper bound.
Therefore S has no least upper bound, even though it is
bounded above.
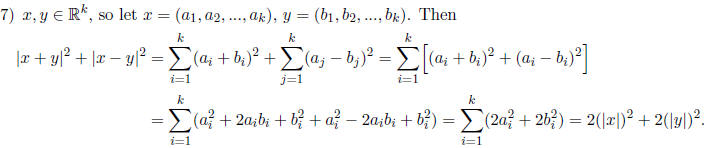
The geometric interpretation comes from looking at the parallelogram whose
vertices are the
points 0, x, x + y and y. Then the equation states that the sum
of the squares of the lengths
of the two diagonals (the vectors x + y and x - y)
is the same as the sum of the squares of the
lengths of the four sides.
| Prev | Next |