A parent guide to mathematics
Tips and Activities for Parents
• Play games with your child such as checkers, board games, chess and increasingly complex card games. All involve problem solving and logic , and all are based on mathematics.
• Present a problem to your child such as finding the number of games to be played in a tournament with 60 teams. Have him or her come up with different strategies to solve the problem.
• Find tables of salaries of possible careers for your child from newspapers, magazines and the Internet and have your child compare the data and draw conclusions.
The math for 7th grade focuses on extending students’ knowledge of fractions to rational numbers and developing concepts of linear equations. Based on national curriculum recommendations and reflecting Ohio Academic Content Standards, the following describes some of the central mathematical skills and understandings that students should acquire by the end of seventh grade.
Number and Operations
Rational Numbers , Roots, and Proportions
1. Add, subtract , multiply, and divide positive and negative rational numbers
(e.g., 1/2 + 3/4 = 1/4; 0.06 × 5 = 0.30)
2. Solve single and multi- step problems using positive and negative rational numbers
3. Understand and solve problems involving proportions, including scaling, unit conversion, rates of change, and equivalence (e.g., convert feet per second to miles per hour, scale a drawing where 1 inch = 10 feet)
4. Understand the meaning of square roots and cube roots;
recognize simple square roots and cube roots, such as
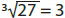 and
and 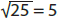 . Use
calculators and prior knowledge to estimate other square roots and cube roots
(e.g.,
. Use
calculators and prior knowledge to estimate other square roots and cube roots
(e.g., 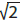 is about 1.4)
is about 1.4)
Linear Relationships
5. Recognize when the information in an applied situation, table, graph or formula suggests a linear relationship between two quantities and understand that it can be represented graphically by a straight line and as a linear equation
6. Solve problems that involve a linear relationship by using graphs and by using equations
7. Find the slope and the
x- and y-intercepts of a line and interpret them for the context in which the linear relationship arises8. Understand that when one quantity varies directly with respect to another quantity, this is a special case of a linear relationship; it may be represented graphically by a straight line through the origin and may be represented by an equation of the form
y = mx (e.g., as the side of a square (s) increases, the perimeter P of the square increases, as P = 4s)9. Solve equations of the form
ax + b = cx + d and justify and interpret the solutions (e.g., the solution to 3x + 10 = 5x – 22 is x = 16)Geometry
Similarity and Construction
10. Draw and construct geometric shapes with specified dimensions
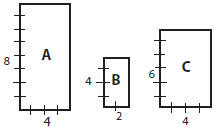
11. Understand the concept of similar polygons and solve related
problems (e.g., rectangles A and B are similar because the ratios of the
corresponding sides in each are equal; 8/4 = 4/2 = 2/1 ; A and C are not similar
because the ratios are not equal; 8/4 ≠ 6/4
Data and Probability
Represent and Interpret Data
12. Represent and interpret data using a variety of graphs and select appropriate graphs to address specific questions
13. Create and interpret scatter plots and when appropriate model the relationship with a line
14. Find and interpret measures of center (median and mean) and variability (range) for a given set of data
Congruent – exactly the same shape and size
Expression – a sequence containing numbers, symbols and operations that can be used to represent a quantity (e.g., 3x + 5)
Equation – a sentence stating that two mathematical expressions are equal (e.g., 2x + 6 = 20 or 4x + 4 = x + 16)
Integers – whole numbers and their opposites (. . . , -3, -2, -1, 0, 1, 2, 3, … )
Intercept
– the value of x or y in
an ordered pair describing the point where a graph intersects the x- or y-axis
(e.g., the x-intercept is at (2, 0) and the y-intercept is at (0, 3) in the
graph shown)
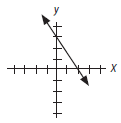
Linear Equation in Two Variables – an equation in two variables whose graph is a straight line (e.g., y = 2x + 3)
Proportion – an equation stating that two ratios are equal (e.g., 3/4 = 15/20)
Rational Numbers – a number that can be expressed as a/b where a and b are integers and b is nonzero (e.g., 3/8, 7 = 7/1, and 6.3 = 63/10)
Root: Square (Cube) – a square (cube) root of a number is a factor of the number whose square (or cube) equals the number (e.g., the cube root of 125 is five because 53 = 5 × 5 × 5 or 125; the square root of 16 is 4 and -4 because is 42= 4 × 4 = 16 and -42= -4 × -4 = 16)
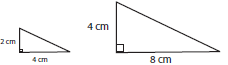
Similar Figures
– figures whose
corresponding sides are proportional and whose corresponding angles are
congruent (e.g., all squares are similar)
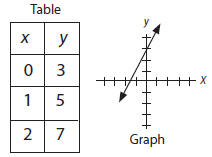
Slope
– the measure of steepness of a
line going from left to right. Numerical value for slope is found using two
points on the line and dividing the change in
y-value
by the change in x-value;
slope = 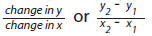 (e.g., to calculate the slope
for y = 2x + 3,
using two points on the line (0, 3) and (1, 5),
(e.g., to calculate the slope
for y = 2x + 3,
using two points on the line (0, 3) and (1, 5),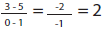
| Prev | Next |