A Quick Review of Elementary Euclidean Geometry
0.5 THE EXTERIOR ANGLE THEOREM
There is an inequality regarding the angles in a triangle that is of
fundamental
importance in many of the proofs of elementary geometry. The theorem is known
as the Exterior Angle Theorem and it is Euclid’s Proposition I.16.
Let ΔABC be a triangle. At each vertex of the triangle
there is an interior
angle and two exterior angles. The interior angle at A is the angle
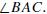 The two
The two
angles 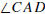 and
and
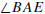 shown in Figure 0.3 are the exterior angles
at A. Note that
shown in Figure 0.3 are the exterior angles
at A. Note that
the two exterior angles at a vertex form a vertical pair and are therefore
congruent.
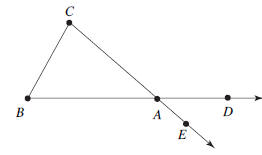
FIGURE 0.3: At each vertex there is one interior angle and there are two
exterior angles
Exterior Angle Theorem. The measure of an exterior angle
for a triangle is strictly
greater than the measure of either remote interior angle.
0.6 PERPENDICULAR LINES AND PARALLEL LINES
Two lines ℓ and m are perpendicular, written ℓ ⊥ m, if they intersect at
right angles.
If ℓ is a line and P is any point, then there is exactly one line m such that P
lies on m
and m ⊥ ℓ. The point at which m intersects ℓ is called the foot of the
perpendicular
from P to ℓ. In case P lies on ℓ, P itself is the foot of the perpendicular. The
process of constructing the perpendicular m is called dropping a
perpendicular—see
Figure 0.4. Euclid proved that it is possible to construct the unique
perpendicular
with compass and straightedge (Proposition I.12).
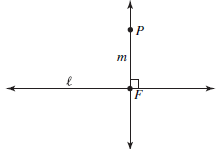
FIGURE 0.4: F is the foot of the perpendicular from P to `
Two lines ℓ and m in the plane are parallel, written ℓ
 m, if they do not
m, if they do not
intersect. It is the existence and uniqueness of parallels that distinguishes
Euclidean
geometry from non-Euclidean geometries. The Euclidean parallel property is
stated
most succinctly in the following postulate.
Playfair’s Postulate. For every line ℓ and for
every point P that does not lie on ℓ there
exists exactly one line m such that P lies on m and m
 ℓ.
ℓ.
In the presence of the other axioms of geometry,
Playfair’s Postulate is
equivalent to Euclid ’s Fifth Postulate. The next two theorems relate parallelism
to
angle congruence. The two theorems are a standard part of high school geometry
and are also Propositions I.27, and I.29 in Euclid. It is in the proof of
Proposition I.29
that Euclid first uses his fifth postulate.
Let ℓ and ℓ' denote two lines in the plane. A transveral
for the two lines
is a line t such that t intersects ℓ and 
 ℓ'
in distinct points. The transversal
ℓ'
in distinct points. The transversal
makes a total of eight angles with the two lines—see Figure 0.5. The two pairs
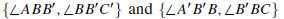 are called alternate interior angles. The
are called alternate interior angles. The
angles 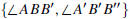 are corresponding angles. There are
three other pairs of
are corresponding angles. There are
three other pairs of
corresponding angles defined in the obvious way.
FIGURE 0.5: Angles formed by two lines and a transversal
Alternate Interior Angles Theorem. If ℓ and ℓ' are
two lines cut by a transversal t in
such a way that a pair of alternate interior angles is congruent, then ℓ is
parallel to ℓ'.
Converse to the Alternate Interior Angles Theorem.
If two parallel lines are cut by
a transversal, then both pairs of alternate interior angles are congruent.
EXERCISES
0.6.1. Prove the following theorem (Euclid’s Proposition I.28).
Corresponding Angles Theorem. If ℓ and ℓ' are lines cut by a transversal
t in such
a way that two corresponding angles are congruent, then ℓ is parallel to ℓ'.
0.6.2. Prove the following theorem (Euclid’s Proposition I.32).
Angle Sum Theorem . For every triangle, the sum of the measures of the
interior
angles of the triangle is 180° .
[Hint: Let ΔABC be a triangle. Draw a line through C that is parallel to the
line
through A and B. Then apply the Converse to Alternate Interior Angles.]
0.7 THE PYTHAGOREAN THEOREM
The Pythagorean theorem is probably the most famous theorem in all of
geometry;
it is the one theorem that every high school student remembers. For Euclid it
was
the culmination of Book I of the Elements. The theorem is named for Pythagoras
of
Samos who lived from about 569 to 475 BC. Few details about the life of
Pythagoras
are known, so it is difficult to determine whether Pythagoras really did prove
the
theorem that bears his name or what kind of proof he might have used.
Notation. Let ΔABC be a triangle. It is standard to
use lower case letters to denote
the lengths of the sides of the triangle: a = BC, b = AC, and c = AB.
Pythagorean Theorem. If ΔABC is a right triangle
with right angle at vertex C, then
a^2 + b^2 = c^2.
Euclid gave two kinds of proofs of the Pythagorean
theorem; the first one
based on area and then later another based on similar triangles.
0.8 SIMILAR TRIANGLES
The similar triangles theorem is one of the most useful in elementary
Euclidean
geometry. Euclid did not prove it, however, until Book VI of the Elements. (The
similar triangles theorem is Euclid’s Proposition VI.4.) The reason he waited so
long is that the ancient Greeks had trouble dealing with the irrational ratios
that
can arise when similar triangles are compared. It is believed that Eudoxus of
Cnidus
(408–305 BC) was the first to give a complete proof of the theorem.
Triangles ΔABC and ΔDEF are similar if ∠ABC
 ∠DEF, ∠BCA
∠DEF, ∠BCA
 EFD,
EFD,
and ∠CAB 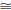 ∠FDE. Write ΔABC
∠FDE. Write ΔABC
 ΔDEF if ΔABC is similar to ΔDEF. As
ΔDEF if ΔABC is similar to ΔDEF. As
with congruence of triangles, the order in which the vertices are listed is
significant .
Similar Triangles Theorem. If ΔABC and ΔDEF are two triangles such that
ΔABC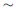 ΔDEF, then
ΔDEF, then
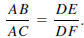
EXERCISES
0.8.1. Prove the following theorem. It is a special case of the Parallel
Projection
Theorem [16, Theorem 7.3.1] and will prove to be very useful later.
Euclid’s Proposition VI.2. LetΔABC be a triangle, and letDandEbe points
on the
sides 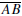 and
and 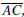 respectively. Then
respectively. Then
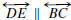 if and only if AD/AB = AE/AC.
if and only if AD/AB = AE/AC.
[Hint for converse: Assume AD/AB = AE/AC. Let ℓ be the line through D
such that 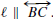 Use Pasch’s Axiom to prove that
there is a point E' where ℓ
Use Pasch’s Axiom to prove that
there is a point E' where ℓ
intersects 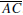 . Prove that E' = E.]
. Prove that E' = E.]
0.8.2. Prove the following theorem (Euclid’s Proposition VI.6).
SAS Similarity Criterion. If ΔABC and ΔDEF are two triangles such that
∠CAB
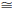 ∠FDE and AB/AC = DE/DF, then ΔABC
∠FDE and AB/AC = DE/DF, then ΔABC
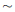 ΔDEF.
ΔDEF.
[Hint: If AB = DE, the proof is easy. Otherwise it may be assumed that AB > DE
(explain). Choose a point B' between A and B such that AB' = DE and let m be
the line through B' that is parallel to
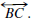 Prove that m intersects
Prove that m intersects
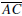 in a point
in a point
C' such that ΔAB'C'
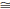 ΔDEF.]
ΔDEF.]
0.9 QUADRILATERALS
Four points A, B, C, and D such that no three of the points are collinear
determine
a quadrilateral, which we will denote by ϖABCD.
Specifically,
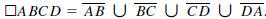
It is usually assumed that the sides
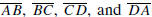 intersect only at their
intersect only at their
endpoints, but we will relax that requirement later in the course.
The four segments are called the sides of the quadrilateral and the points
A,B,C, and D are called the vertices of the quadrilateral. The sides
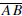 and
and
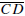
are called opposite sides of the quadrilateral as are the sides
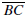 and
and
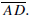 Two
Two
quadrilaterals are congruent if there is a correspondence between their vertices
so
that all four corresponding sides are congruent and all four corresponding
angles
are congruent.
There are several special kinds of quadrilaterals that
have names. A trapezoid
is a quadrilateral in which at least one pair of opposite sides is parallel. A
parallelogram is a quadrilateral in which both pairs of opposite sides are
parallel. It
is obvious that every parallelogram is a trapezoid, but not vice versa. A
rhombus is
a quadrilateral in which all four sides are congruent. A rectangle is a
quadrilateral
in which all four angles are right angles. A square is a quadrilateral that is
both a
rhombus and a rectangle.
EXERCISES
0.9.1. Prove the following theorem.
Euclid’s Proposition I.34. The opposite sides of a parallelogram are
congruent.
[Hint: Draw a diagonal and use ASA.]
0.10 CIRCLES AND INSCRIBED ANGLES
Let r be a positive number and let O be a point. The circle with center O
and radius r
is defined by C(O, r) = {P | OP = r}. The diameter of the circle is d = 2r.
While
the radius of a circle is usually thought of as a number, it is often convenient
to refer
to one of the segments
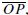 P ∈ C(O, r), as a radius of the circle C(O, r). In the
P ∈ C(O, r), as a radius of the circle C(O, r). In the
same way, a segment
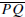 such that P and Q lie on the circle and O ∈
such that P and Q lie on the circle and O ∈
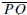 is called a
is called a
diameter of C(O, r).
Let γ be a circle and let P be a point on γ . A line t is tangent to γ at P if
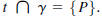
Tangent Line Theorem. Let γ = C(O, r) be a circle
and let ℓ be a line that intersects
γ at P. Then ℓ is tangent to r at P if and only if
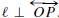
Let γ = C(O, r) be a circle. An inscribed angle for
γ is an angle of the form
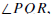 where P,Q, and R all lie on γ. The arc
intercepted by the inscribed angle
where P,Q, and R all lie on γ. The arc
intercepted by the inscribed angle
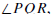 is the set of points on γ that lie in the
interior of
is the set of points on γ that lie in the
interior of 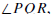 .
.
Inscribed Angle Theorem. If two inscribed angles intercept the same arc,
then the
angles are congruent.
The inscribed angle theorem is Euclid’s Proposition III.21.
EXERCISES
0.10.1. Prove the following theorem. It is Euclid’s Proposition III.3.
Secant Line Theorem. If γ = C(O, r) is a circle and ℓ is a line that
intersects at
distinct points P and Q, then O lies on the perpendicular bisector of the chord
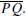
0.10.2. Prove the following theorem.
External Tangents Theorem. If γ = C(O, r) is a circle and ℓ and m are two
nonparallel lines that are tangent to γ at the points P and Q, and A is the
point of
intersection of ℓ and m, then PA = QA.
0.10.3. The following theorem can be viewed as a special
case of the Inscribed Angle Theorem.
Give a proof that does not use the Inscribed Angle Theorem. The theorem
is named for Thales of Miletus (624–547 BC); it is Euclid’s Proposition III.31.
Thales’ Theorem. If the vertices of ΔABC lie on a circle and
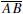 is a diameter of
is a diameter of
that circle, then 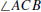 is a right angle.
is a right angle.
[Hint: Let O be the midpoint of 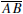 . Observe
that AO = BO = CO and apply
. Observe
that AO = BO = CO and apply
the Isosceles Triangle Theorem along with the Angle Sum Theorem.]
0.10.4. Prove the following theorem.
Converse to Thales’ Theorem. If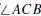 is a
right angle, then the vertices of ΔABC
is a
right angle, then the vertices of ΔABC
lie on a circle and 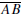 is a diameter of that
circle.
is a diameter of that
circle.
[Hint: Again let O be the midpoint of 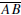 . There
is a point C' such that C' lies on
. There
is a point C' such that C' lies on
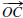 and OC' = OA. Show that the assumption C ≠
C' leads to a contradiction.]
and OC' = OA. Show that the assumption C ≠
C' leads to a contradiction.]
0.10.5. Use the angle sum theorem and the linear pair
theorem to prove the following
result: If ΔABC is a right triangle with right angle at C and O is the midpoint
of
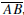 then
then 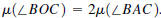 This
theorem is a special case of the Central
This
theorem is a special case of the Central
Angle Theorem [16, Theorem 10.4.9]. It will be used repeatedly in later
chapters.
0.11 AREA
A polygon is a generalization of triangle and quadrilateral. A polygon P has
a finite
set of vertices A1,A2, ... ,An. The polygon is defined by
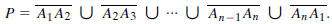
The segments 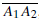 etc., are called the sides of
the polygon. The sides of a polygon
etc., are called the sides of
the polygon. The sides of a polygon
are one-dimensional and have no area. Corresponding to each polygon in the plane
there is a region, which consists of the points of the polygon itself together
with the
points inside the polygon. It is the region that is
two-dimensional and has area. The
distinction between the polygon and the corresponding polygonal region will be
important in this course because Geometer’s Sketchpad treats the two as
different
objects that must be constructed separately.
For each polygonal region in the plane there is a
nonnegative number called
the area of the region. The area of a region R is denoted by .α(R). The area of a
triangular region is given by the familiar formula
area = (1/2)/base × height.
The other important property of area is that it is additive , which means that
the area
of a region that is the union of two nonoverlapping subregions is the sum of the
areas if the subregions.
EXERCISES
0.11.1. Prove that the area of a triangle ΔABC is given by the formula
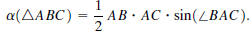
| Prev | Next |