Algebra Review
1 Groups
Definition 1.1 A semigroup (G, ·) is a set G with a binary operation ·
such that:
Axiom 1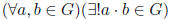 
Axiom 2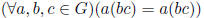 
Definition 1.2 A group (G, ·) is a semigroup such that:
Axiom 3 (Identity element)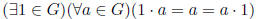 
Axiom 4 (Inverse)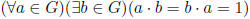 
Multiplicative Notation :
• ab = a · b
• In Axiom 4, b = a-1
Additive Notation :
• Binary operation ‘+’
• Identity becomes ‘0’
• Additive inverse ‘-a’
The size of G as a set, which is denoted |G|, is called the order of G.
Definition 1.3 G is an abelian group if G is a group such that
.
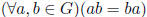Definition 1.4 H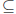 
G is a
subgroup of G (denoted H ≤ G) if
1. 1 ∈ H
2. H is closed under the binary operation
3. H is closed under inverses
Definition 1.5 Let H ≤ G. The sets of the form a ·H := {ah : h ∈ H} for a ∈G are
the left
cosets of G. The left cosets partition G. Right cosets are defined analogously.
Definition 1.6 |G : H| = number of left cosets of H in G is called the index of
H in G.
Exercise 1.7 Prove that the number of left cosets is the same as the number of
right cosets,
even if G is infinite. (Hint: construct a bijection between the left and the
right cosets.)
Exercise
1.8 Prove: if G is finite then the left and the right cosests have a
common system
of represetatives, i. e., there exists a set T of size |T| = |G : H| such that T
contains exactly
one element from every left coset as well as from every right coset.
Exercise 1.9 (Lagrange) If H ≤ G then |G| = |H| · |G : H|. Therefore, if |G| <
∞
then
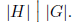
Exercise 1.10 Prove: the intersection of subgroups is a subgroup.
Definition 1.11 Let S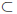 
G. We define the subgroup of G
generated by S by
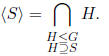
A group is cyclic if it is generated by an element (|S| = 1).
Exercise 1.12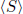 
is the set of all products of elements of S and inverses of
elements of S.
Example 1.13 Let S = {a, b}. Then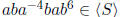 
.
Example 1.14 If |S| = 1 and S = {g} then
.
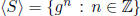Exercise 1.15 If G is cylic then
1. if |G| = 1 then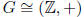 
2. if |G| = n then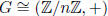 
Definition 1.16 The order of an element g ∈ G is the order
of the cyclic group generated
by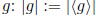 
.
Exercise 1.17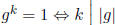 
Exercise 1.18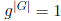 
Exercise 1.19 (Euler - Fermat)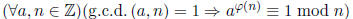 
Exercise 1.20 If G is an abelian group then
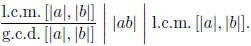
This shows that if g.c.d. [|a|, |b|] = 1 then |ab| =
l.c.m. [|a|, |b|].
Definition 1.21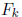 
is a free group of rank k on
free generators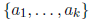 
if the
products of the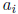 
and the
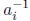give 1 only by explicit cancellation.
Example 1.22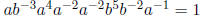 
Exercise+ 1.23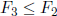 
. In fact,
.
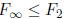Definition 1.24 For a commutative ring R, the special linear group SL(n,R) is
the group
of those n × n matrices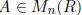 
with det(A) = 1. (More about rings below; we
assume all
rings have an identity element.)
Exercise* 1.25 (Sanov)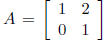 
and AT (A transpose)
freely generate a free group
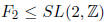. (Hint: for
, let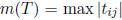 
. Show that
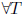there is
at most one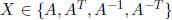 
such that m(T) ≥ m(TX).)
Definition 1.26 Let G be a group and S
G \ 1. The Cayley graph
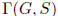has G
for its
vertex set ; elements g, h ∈ G are adjacent if
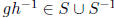(where 
).
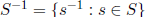Exercise 1.27 Prove: 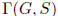is connected if and only if S generates G.
Exercise 1.28 Suppose G =
. Then
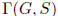is bipartite if and only if G has a
subgroup
N of index 2 such that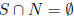 
;.
Exercise 1.29 Let S be a minimal set of generators of G, i. e., no proper subset
of S generates
G. Prove: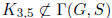 
.
A theorem of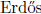 
and Hajnal states that if an
(infinite) graph X does not contain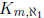 
as
a subgraph (for some m ∈N) then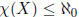 
. As a consequence of the preceding
exercise , if
S is a minimal set of generators then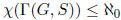 
.
Exercise 1.30 Prove that every group G has a set S of generators such that
.
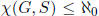Hint. Not every group has a minimal set of generators (e. g., (Q, +) does not).
But every
group has a sequentially non-redundant set of generators,
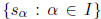, where I is
a well-ordered
set and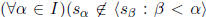 
. Prove that if S is sequentially non-redundant
then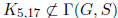 
.
Exercise 1.31 If a regular graph of degree r with n vertices has girth g then
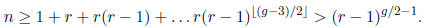
Consequently,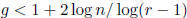 
.
On the other hand, and Sachs proved for every r ≥ 3 there exist r-regular
graphs of girth
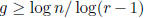. The following problem addresses the question of explicit
construction
of a 4-regular graph with large girth. The girth will be optimal within a
constant factor .
Exercise 1.32 (Margulis) Let G = SL(2, p) := SL(2,Z/pZ). Let S = {A,B} where
and B = AT (A transpose). Note that |G| < p3 and has degree 4. Prove
that the girth of is
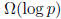. (Hint. Use Sanov's Theorem and the submultiplicativity
of matrix norm.
2 Rings
Definition 2.1 A ring (R,+, ·) is an abelian group (R, +) and semigroup (R, ·)
such that:
• ( Distributivity )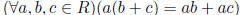 
and ((b + c)a = ba + ca)
Exercise 2.2 In a ring R,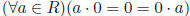 
Definition 2.3 (R,+, ·) is a commutative if (R, ·) is abelian.
Definition 2.4 R is a ring with identity if (R, ·) satisfies Axiom 3 (semigroup
with identity)
and 1 ≠ 0.
CONVENTION. By “rings” we shall always mean rings with identity.
Definition 2.5 a ∈ R is a unit if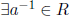 
.
Exercise 2.6 The units of R form a multiplicative group
denoted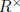 
.
Example 2.7 Let R be a ring.
• 
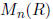:= set of n × n matrices over R is a ring
Exercise 2.8 Let R be a commutative ring. GL(n,R) denotes the group of units of
.
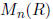Prove: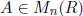 
belongs to GL(R) if and only if
.
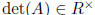Example 2.9 mod m residue classes form a ring, denoted Z/mZ.
Exercise 2.10 What is the order of the group of units of Z/mZ?
Definition 2.11 a ∈ R is a left zero divisor if a ≠ 0 and
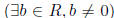(ab =
0). Right
zero divisors are defined analogously.
Definition 2.12 a ∈R is a zero-divisor if a is a left OR a right zero-divisor.
Exercise 2.13
1. If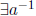 
then a is not a zero-divisor.
2. The coverse is false.
3. The converse is true if R is finite.
4. The converse is true if
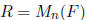where F is a field. In this case, A ∈ R is
a zero-divisor
if and only if det(A) = 0.
Definition 2.14 An integral domain is a commutative ring with no zero-divisors.
Definition 2.15 A division ring is a ring where all nonzero elements are units, i.
e.,
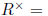
R \ {0}.
| Prev | Next |