Algebraic Symmetries
III. Neue Entdeckungen.
Es ist jedem 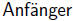 der Geometrie bekannt, dass
der Geometrie bekannt, dass
verschiedene ordentliche Vielecke, namentlich das
Dreyeck, Viereck, Funfzehneck, und die,welche durch
wiederholte Verdoppelung der Seitenzahl eines derselben
entstehen, sich geometrisch construiren lassen. So weit
war man schon zu Euklids Zeit, und es scheint, man habe
sich seitdem allgemein 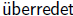 , dass das Gebiet der
, dass das Gebiet der
Elementargeometrie sich nicht weiter erstrecke: wenigstens
kenne ich keinen 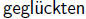 Versuch, ihre Grenzen
Versuch, ihre Grenzen
auf dieser Seite zu erweiten.
Desto mehr, 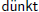 mich, verdient die Entdeckung
mich, verdient die Entdeckung
Aufmerksamkeit, dass ausser jenen ordentlichen Vielecken
noch eine Menge anderer, z. B,. das Siebenzehneck, einer geometrischen
Construction 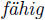 ist. Diese Entdeckung ist
ist. Diese Entdeckung ist
eigentlich nur ein Corollarium einer noch nicht ganz vollendeten
Theorie von 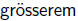 Umfange, und sie soll,
Umfange, und sie soll,
sobald diese ihre Vollendung erhalten hat, dem Publicum
vorgelegt werden.
C. F. Gauss, a. Braunschweig,
Stud. der Mathematik zu 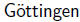 .
.
Es verdient angemerkt zu werden, dass Hr. Gauss
jetzt in seinem 18ten Jahr steht, und sich hier in Braunschweig
mit eben so gl¨ucklichem Erfolg der Philosophie
und der classischen Litteratur als der 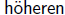 Mathematik
Mathematik
gewidmet hat.
Den 18 April 96.
E. A. W. Zimmermann, Prof.
Die Allgemeine Literatur-Zeitung
From Meyers  Lexikon:
Lexikon:
This review appeared in Jena from 1785 to 1803 and in Halle from 1804 to 1849
and
was a leading organ of German classical and romantic literature. Goethe,
Schiller and
Kant were among the editors and authors. It moved to Halle as a result of an e
ort of
the romantics to increase their control over the review and was replaced in
Jena, on the
initiative of Goethe by the Jenaische Allgemeine Literatur-Zeitung.
Gauss
Gauss, who was born in 1777, wrote the Disquisitones between 1796 and 1798, thus
between his nineteenth and twenty- first years. It did not appear until 1801. It
contains a
great deal in the way both of theorems and theories, the most important being:
1. Proof of law of quadratic reciprocity. The statement was already known at
the
time, but even the best of the eighteenth century mathematicians were unable to
find a
proof. It remains a central mathematical theorem.
2. Developed the theory of binary quadratic forms. In particular, he
introduced
the notion of composition of quadratic forms and established its properties .
Although
in some respects, namely in the context of the notion of ideal number,
composition has
become a common working tool of all algebraists and number -theorists, Gauss's
theory
itself is still difficult and little known. His form of the theory would appear
to be that best
suited to computation.
3. Cyclotomic fields. The construction of the regular heptadecagon, and,
more generally,
the analysis of the numbers formed from roots of unity . This is thus one of the
earliest manifestations of Galois theory. Gauss presumably knew more than he
included
in the book, but he, apparently, published very little more on the subject.
His thesis of 1799 established, in effect and for the first time, that every
polynomial
equation has a root.
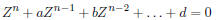
As the root may be complex and the thesis did not refer to
complex numbers, the formulation
of the thesis was necessarily somewhat different . I have already emphasized that
this
is a basic mathematical fact.
These are all theories and results to which the contributions of Gauss are
clear. In
addition , he appears to have occupied himself as a very young man, even as an
adolescent,
with other important problems and observations, for example, with the nature of
geometries
in which the parallel axiom of Euclid is not satisfied and with the
arithmetic -geometric
mean, which is both an elementary and an advanced topic. Here, however, the
evidence is
different. It consists of Gauss's recollections as a somewhat saturnine older
man, so that
it appears to be difficult to disentangle what he himself discovered later, what
he learned
from other authors as an adolescent { he had an early and extensive acquaintance
with the
work of various leading eighteenth century mathematicians { as well as what he
learned
later, from what he discovered early. One could certainly spend a lot of time
with Gauss's
Collected Works and with his correspondence, reflecting on these matters.
One extremely useful reference is a diary that Gauss kept between 1796 and 1814,
with 146 entries that record his principal discoveries. The lemniscate function
to which, as
I noticed, Gauss alludes in the first lines of chapter 7 of the Disquisitiones
appears several
times . I was asked what Gauss what may have meant with his allusion to the
lemniscate.
A brief examination of the diary and of the collected works, which contain ample
editorial
comments, makes perfectly clear what Gauss knew. Although it is a digression
from my
main purpose, it is worthwhile to tarry a little on the matter.
The goal of this year's lectures is after all to communicate, starting at the
beginning,
some genuine mathematical understanding, beyond the gee-whiz or what I refer to
as the
Jack Horner manner, of recent achievements in number theory, and it would be a
shame,
since we are now in a position to appreciate a more detailed explanation of
Gauss's allusion,
to let slip the occasion of acquiring more concrete information.
Gauss was an overwhelming presence in nineteenth century mathematics, Even
though
he exerted little active influence. The German pre-eminence in mathematics as a
whole,
and in certain domains such as number theory in particular, that lasted
throughout the
nineteenth century and until the early thirties is due in good part to him,
although the
Prussian university system was probably also a significant factor. I have not
studied these
matters. Oddly enough it appears to have been  Weil who was most thoroughly
Weil who was most thoroughly
imbued with the aspirations of German number theory, both through direct,
personal
experience as a young man during the twenties and through his studies of variou
nineteenth
century authors. Simplifying, for the purposes of brevity, an elaborate
development in
which a large number of mathematicians took part, one might say that he not only
brought
it intact through the war at its highest level but also was the principal source
of its
transformation into the theories that were finally and successfully exploited in
the proof
of Fermat's theorem.
His major contribution was, oddly enough, a set of conjectures, the Weil
conjectures,
now demonstrated, but by others. He is, in various comments to his papers, quite
explicit
about the relation of these conjectures to Gauss and the lemniscate.
I quote from Weil's Two lectures on number theory, past and present, an essay I
recommend to your attention.
"In 1947, in Chicago, I felt bored and depressed and, not knowing what to do, I
started reading
Gauss's two memoirs on biquadratic residues, which I had never read
before....This
led me in turn to some conjectures."
A few lines later Weil draws attention to the very last
entry in Gauss's diary, an entry to
which we shall come in a moment.
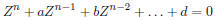
Digression
The digression at first sight seems to demand some knowledge of the
calculus, but it does not. I first write down a formula that may be familiar
to some, but not to all. No matter! Do not puzzle over the left side. It is
no more than the mathematician's usual fastidious way of writing down the
length of the arc from the point (1, 0) on the circle to the point (x, y) and
that is what we mean by θ, which of course has to be measured in radians,
thus in units in which the radius is 1, but that is the unit chosen. If

then y = sin( θ). If y = 1 then θ= π/2.
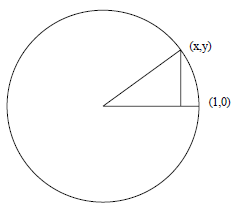
We now do something similar for the lemniscate, a curve
defined by the
equation
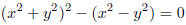
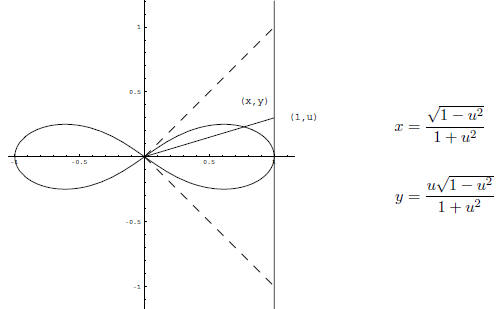
The lemniscate is the curve in the form of a bow. The
point (x, y) is the
point where the line through the points (0, 0) and (1, u) cut the curve. The
length of the curve from (1, 0) to the point (x, y) is expressed mathematically
as

Once again, there is no need to be troubled by the
integral. It is again just a
way of expressing the length of an arc of a curve. Observe that θ plays
here
the role of the angle in a circle measured in radians. Gauss wrote
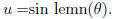
If u = 1, then θ is some number that I call, following Gauss,
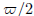 . Thus
. Thus
 is the length of the upper loop on the right
running from (1, 0) to (0, 0).
is the length of the upper loop on the right
running from (1, 0) to (0, 0).
Constructing a regular triangle, a regular pentagon, or a
regular heptadecagon
is the problem of dividing the total circumference of the circle into
three, five or seventeen arcs of equal length. We could consider the same
problem for the lemniscate, taking the initial point, which is now important
as it was not, because of symmetry, for the circle, to be the point (0, 1). In
an entry for March 19, 1797 Gauss notes that this leads to an equation for
u of degree m2, whereas for the circle it was an equation of degree
m. In
the cases already considered, m was 3 or 5. We remove one easy root, u = 0
corresponding to the first point of division. This leads to equations of degree
m − 1 or for a lemniscate m2 − 1. In a later entry, apparently for
April 15,
he observes there is a problem of separating the real roots of this equation
from the complex. He is seeking the real roots. The corresponding equation
for the circle, thus for y, has only real roots. It is the numbers x + iy that
are complex. The real roots of the equation of degree m2−1 give the
division
points and there are m− 1 of them.
In an entry dated March 21, he observes implicitly (all the entries are
cryptic) that these m − 1 roots are numbers that can be constructed with a
ruler and compass .
| Prev | Next |