Classification and Linear Equations
These notes cover some of the material that we covered in
class on first-order ordinary
differential equations . As the presentation of this material in class was
somewhat different
from that in the book, I felt that a written review closely following the class
presentation
might be appreciated.
1. Introduction, Classification, and Overview
1.1. Introduction. A differential equation is an algebraic relation
involving derivatives
of one or more unknown functions with respect to one or more independent
variables, and
possibly either the unknown functions themselves or their independent variables,
that hold
at each point in the domain of those functions.
For example, an unknown function p(t) might satisfy the relation

This is a differential equation because it involves the
derivative of the unknown function
p. It also involves the value of p , but not the independent variable t. It is
understood that
this relation should hold every point t where p(t) and its derivative are
defined.
Similarly, unknown functions u(x, y) and v(x, y) might satisfy the relation

where 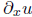 and
and
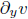 denote partial derivatives. This is a
differential equation because it
denote partial derivatives. This is a
differential equation because it
involves derivatives of the unknown functions u and v. It does not involve
either the values
of u and v or the independent variables x and y . It is understood that this
relation should
hold every point (x, y) where u(x, y), v(x, y) and their partial derivatives
appearing in (1.2)
are defined.
Here are other examples of differential equations that involve derivatives of a
single
unkown function:
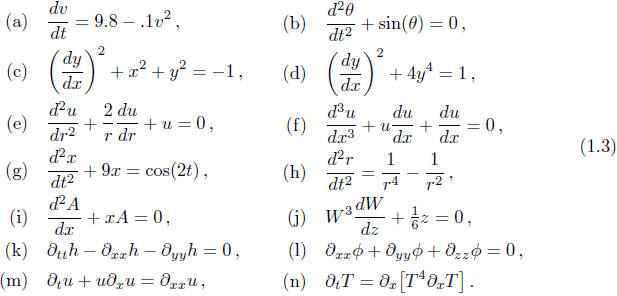
In all of these examples except k and l the unknown
function itself also appears in the
equation. In examples d, e, g, i, and j the independent variable also appears in
the equation.
1.2. Classification. A differential equation is called an ordinary
differential equation
(ODE) if it invloves derivatives with respect to only one independent variable.
Otherwise,
it is called a partial differential equation (PDE). Example (1.1) is an ordinary
differential
equation. Example (1.2) is a partial differential equation. Of the examples in
(1.3):
a – j are ordinary differential equations ;
k – n are partial differential equations .
The order of a differential equation is the order of the highest derivative that
appears
in it. An nth-order differential equation is one whose order is n. Examples
(1.1) and (1.2)
are both first-order differential equations. Of the examples in (1.3):
a, c, d, j are first-order differential equations ;
b, e, g, h. i, k, l, m, n are second-order differential equations ;
f is a third-order differential equation .
A differential equation is said to be linear if each side of the equation is a
sum of
terms, each of which either
• is a derivative of an unknown function times a factor that is independent of
the
unknown functions,
• is an unknown function times a factor that is independent of the unknown
fuctions,
• or is entirely independent of the unknown fuctions.
Otherwise it is said to be nonlinear. Examples (1.1) and (1.2) are both linear
differential
equations. Of the examples in (1.3):
e, g, i, k, l are linear differential equations ;
a – d, f, h, j, m, n are nonlinear differential equations .
Every nth order linear ordinary differential equation for a single unknown
function y(t)
can be brought into the form
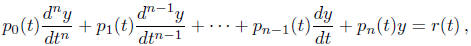
where 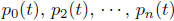 , and r(t) are
given functions of t such that p0(t) ≠ 0. Linear
, and r(t) are
given functions of t such that p0(t) ≠ 0. Linear
differential equations are important because much more can be said about them
than for
general nonlinear differential equations.
In applications one is often faced with a system of coupled differential
equations —
typically a system of m equations for m unknown functions. For example, two
unknown
functions p(t) and q(t) might satisfy the system
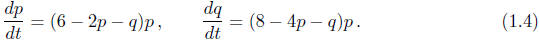
Similarly, two unknown functions u(x, y) and v(x, y) might satisfy the system
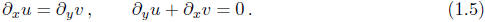
The order of a system of differential equations is the
order of the highest derivatrive
appearing in the entire system. Example (1.4) is a first-order system of
ordinary differential
equations, while (1.5) is a first-order system of partial differential
equations. The size of
the systems that arise in applications can be extremely large. Systems of 108
ordinary
differential equations are being solved every day.
1.3. Course Overview. Differential equations arise in mathematics,
physics, chem-
istry, biology, medicine, pharmacology, communications, electronics, finance,
economics,
areospace, meteorology, climatology, oil recovery, hydrology, ecology,
combustion, image
processing, and in many other fields. Partial differential equations are at the
heart of most
of these applications. You need to know something about ordinary differential
equations
before you study partial differential equations. This course will serve as your
introduction
to ordinary differential equations. More specifically, we will study four
classes of ordinary
differential equations. We illustrate these four classes below denoting the
independent
variable by t.
(I) We will begin with single first-order ODEs that can be brought into the form

These will be covered before the first in-class exam. You
may have seen some of the
material in your calculus courses.
(II) We will next study single nth-order linear ODEs that can be brought into
the form
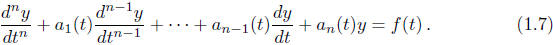
These will be covered before the second in-class exam.
This is the heart of the course.
Many students find this the most difficult part of the course.
(III) We will then turn towards systems of n first-order linear ODEs that can
brought into
the form
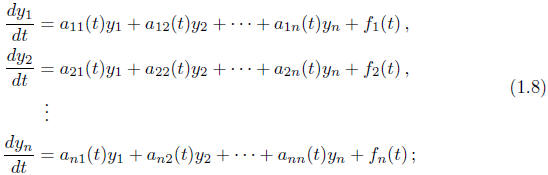
These will be covered before the third in-class exam. This
material builds upon the
material covered in part II.
(IV) Finally, we will study systems of two first-order ODEs that can brought into the form
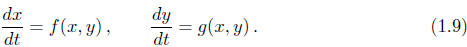
These will be covered before and immediately after the
third in-class exam. This
material builds upon the material in parts I and III.
This is far from a complete treatment of the subject. It will however prepare
you to learn
more about ordinary differential equations or to learn about partial
differential equations.
2. First-Order Equations: Explict and Linear
2.1. Introduction. We now begin our study of first-order ordinary
differential equations
that involve a single real -valued unknown function y(t). These can always be
brought into
the form
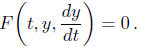
If we try to solve this equation for dy/dt in terms of t
and y then there might be no solutions
or many solutions. For example, equation (c) of (1.3) clearly has no (real)
solutions because
the sum of nonnegative terms cannot add to −1. On the other hand, equation (d)
will be
satisfied if either
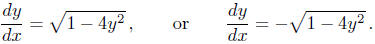
To avoid these complications we will restrict ourselves to
equations that can be brought
into the form

Examples (1.1) and (a) of (1.3) are already in this form.
Example (j) of (1.3) can easily
be brought into this form. And as we saw above, example (d) of (1.3) can be
reduced to
two equations in this form.
We will say that y = Y (t) is a solution of (2.1) over an interval (a, b) whenever
|
(i) the function Y is differentiable over (a, b) , (ii) f(t, Y (t)) is defined for every t in (a, b) , (iii) Y ′(t) = f(t, Y (t)) for every t in (a, b) . |
(2.2) |
Some basic questions we want to address are the following.
• When does (2.1) have solutions?
• Under what conditions is a solution unique?
• How can we find analytic expressions for solutions ?
• How can we visualize solutions?
• How can we approximate solutions?
We will focus on the last three questions. They address practical skills that
you can apply
when faced with a differential equation. The first two questions will be viewed
through
the lens of the last three. They are important because differential equations
that arise in
applications are supposed to model or predict something. If an equation either
does not
have solutions or has more than one solution then it fails to meet this
objective. Moreover,
in those situations the methods by which we will address the last three
questions can give
misleading results. We will therefore study the first two questions with an eye
towards
avoiding such pitfalls. Rather than addressing these questions for a general f(t,
y) in (2.1),
we will start by treating special forms f(t, y) of increasing complexity.
| Prev | Next |