College algebra
Instructor: Prof. Carol Okigbo
Dept: Corrick Center for General Education
Tel: 477 2188
Office: Murray Commons: Room 223H
Class Meeting Time: MWF 10:00 a.m.-10:50 a.m.
Classroom (BD/RM): MU 223N
Office Hours:
Monday & Friday 1:00 p.m. – 4:00 p. m.
Tuesday & Thursday 2:00 p.m. - 4:00 p.m.
Course Objectives: The primary objectives for this
class are to help students to:
 Develop an understanding of problem solving
strategies and skills necessary for
Develop an understanding of problem solving
strategies and skills necessary for
success in the study of higher-level mathematics.
![]() Build and develop
mathematical critical thinking and reasoning skills necessary
Build and develop
mathematical critical thinking and reasoning skills necessary
for solving real - life problems.
![]() Master algebraic
concepts and be able to apply them to mathematics encountered
Master algebraic
concepts and be able to apply them to mathematics encountered
in other disciplines.
![]() Build and develop
sustainable confidence in their ability to solve mathematical
Build and develop
sustainable confidence in their ability to solve mathematical
problems and overcome deficiencies in mathematical language.
Course Description: The course is designed to provide the algebra you
need to be able
to take higher math courses such as Applied Mathematics, Pre-Calculus or
Trigonometry.
The course will aim at covering the following topics: Exponents, factoring ,
equations and
inequalities , functions, exponential and logarithmic functions, systems of
equations, and
matrices. Prerequisite: MDS 100.
Text: Swokowski and Cole (2006). Algebra &Trigonometry with Analytic
Geometry.
Belmont, CA: Thomson Wadsworth.
Instructional Strategies: The approach to this course will be interactive
and active
participation of students is required. It will employ a combination of
strategies that will
include use of white board/transparencies/power point presentation, small group
work,
and class discussion.
Assessment: This will consist of a combination of exams, periodical
homework, in-class
activities and work sheets.
1. Exams
In-class exams: There will be five regular in-class exams and a
comprehensive final exam. The dates for the exams are in the schedule
provided below.
2. Homework: There will be some suggested problems
from each section of the
class textbook. Some problems will be selected from the suggested ones and
assigned periodically for grading. Students are required to access them on the
D2L, print them out and hand them in accordingly (as at when due).
3. In-class Activities: Students get five points for each day they come to class
and
participate actively in class activity.
4. Work Sheets: In addition to the homework problems I will assign also
assign
worksheets that I have made up. These are supplementary work not covered in
homework. Students should print these out from the D2L, complete them and
hand them in accordingly (as at when due).
5. Quizzes and Project: There will be some periodical in-class short
quizzes and at
least one project.
.
Evaluation:
Profile for grade:
Final Exam………….………...20% or 200 points
In-class………………………..10% or 100 points
Chapter Exams. ………...…….40% or 400 points
Homework/Worksheet ……….15% or 150 points
Quiz and project………………15% or 150 points
Credits: 2 ……….. 75% or 750 and above
1……….. 60% or 600 - 74% or 740
Below 60% or 600, no credit
Attendance: The class is interactive and full attendance is expected.
This is the only way
students can get all the 10% or 100 points for in-class.
Special Needs: Any student(s) with disabilities who believe they may need
an
accommodation in this class are encouraged to contact Greg Toutges, Coordinator
of
Disability Services at 477-2652 (phone) or 477-2047 (TTY), CUM 222 as soon as
possible to ensure that accommodations are implemented in a timely fashion.
Academic Honesty: All work in this course must be completed in a manner
consistent
with MSUM Policy. Academic dishonesty in any form is inconsistent with the
university
policy and will not be acceptable. Any verifiable instance of academic
dishonesty may
result in a zero on the assignment , reduction of the final credit evaluation, or
other
appropriate University action
Tentative Class Schedule
| Weeks | Dates | Monday | Wednesday | Friday |
| 1 | Jan. 8 – 12 | No Class | 1.1 | 1.2 |
| 2 | Jan. 15 – 19 | No Class | 1.2 | 1.3 |
| 3 | Jan. 22 – 26 | 1.4 | 1.4 | Exam 1 on Chapter 1 |
| 4 | Jan. 29 – Feb. 2 | 2.1 | 2.2 | 2.2 |
| 5 | Feb. 5 – 9 | 2.4 | 2.3 | 2.4 |
| 6 | Feb. 12 – 16 | 2.5 | 2.6 | 2.7 |
| 7 | Feb. 19 – 23 | 2.7 | Exam on chapter 2 |
3.1 |
| 8 | Feb. 26 – Mar. 2 | 3.2 | 3.3 | 3.4 |
| 9 | Mar. 5 – 9 | 3.7 | 3.7 | Exam on chapter 3 |
| 10 | Mar.12 - 16 | Spring | Break | Break |
| 11 | Mar. 19 - 23 | 5.1 | 5.2 | 5.3 |
| 12 | Mar. 26 – 30 | 5.4 | 5.5 | 5.5 |
| 13 | April 2 – April 6 | 5.6 | 5.6 | Exam on chapter 5 |
| 14 | April 9 - 13 | No Class | 9.1 | 9.2 |
| 15 | April 16 - 20 | 9.5 | 9.6 | 9.7 |
| 16 | April 23 - 27 | 9.8 | 9.9 | Exam on Chapter 9 |
| 17 | April 30 – May 4 | Review for Finals |
Study Day | |
| 18 | May 7 - 11 | Final Exam on Tuesday May 10th @ 12:00 Noon |
Note: Changes may be made as the semester progresses.
| Section | Selected Homework Problems |
| 1.1 | 2, 4, 6, 12, 14, 18, 22, 26, 28, 30, 34, 36, 38, 40, 50, and 52 |
| 1.2 | 4, 6, 8, 14, 16, 18, 22, 28, 32, 42, 44, 48, 50,
54, 60, 64, 70, 74, 78, 82, 84, 86, 88, and 90 |
| 1.3 | 2, 4, 6, 10, 14, 18, 22, 30, 34, 36, 40, 44, 52,
56, 60, 66, 78, 84, 88, 90, 94, 98, and 102 |
| 1.4 | 4, 6, 8, 12, 18, 22, 26, 30, 32, 36, 42, 46, 52, 58, 62, 68, 72, 76, 80 |
| 2.1 | 6, 10, 12, 14, 16, 20, 22, 26, 34, 38, 42, 48, 52, 62, 68 |
| 2.2 | 2, 4, 6, 12, 14, 16, 18, 20, 22, 24, 26, 28, 31, 32, 34 |
| 2.3 | 4, 12, 16, 18, 20, 24, 26, 28, 34, 36, 38, 42, 44, 46, 48, 52, 54, 59, 64, and 70 |
| 2.4 | 2, 4, 12, 16, 18, 20, 24, 26, 32, 34, 36, 38, 42, 44, 46, 48, 52, 54 |
| 2.5 | 4, 6, 8, 12, 20, 28, 43, 40, 42, 46, 48, 50, 52, 54, 58, 60 |
| 2.6 | 4-20 evens, 24, 30, 32, 34, 40, 42, 44, 46, 48, 50, 56, 60, 62, 70, 80 |
| 2.7 | 2, 4, 10, 14, 20, 22, 26, 30, 34, 38, 48 |
| 3.1 | 12, 16, 18, 20, 26, 30 |
| 3.2 | 2, 4, 6, 8, 16, 18, 20, 24, 26, 28, 30, 32, 34, 38, 42, 44, 46, 48, 52, 56 |
| 3.3 | 4, 6, 12, 14, 18, 20, 24, 28, 30, 32, 34, 36, 40, 42, 44, 46, 48, 54, 60 |
| 3.4 | 2, 4, 10, 12, 14, 16, 18, 20, 22, 26, 28, 30, 34, 36, 38, 42, 48, 58, 72 |
| 3.7 | 2, 4, 6, 8, 10, 12, 14, 18, 20, 22, 26, 28, 32, 34, 38, 48, 52, 58, 60 |
| 3.7 | 2, 4, 6, 8, 10, 12, 14, 18, 20, 22, 26, 28, 32, 34, 38, 48, 52, 58, 60 |
| 5.1 | 2, 6, 10, 14, 18, 20, 22, 24, 26, 30, 34, 38, 42, 44, 48, 50 |
| 5.2 | 2, 4, 6, 8, 10, 12, 18, 22, 26, 28, 30, 32, |
| 5.3 | 2, 4, 6, 8, 10, 12, 14, 16, 18, 22, 28, 46, 48, 52, |
| 5.4 | 2, 8, 10, 12, 14, 20, 22, 28, 30, 32, 34, 50, 56, 60 |
| 5.5 | 2, 4, 12, 18, 20, 22, 28, 34, 40, 46, 48, 52, 58, 60, 64 |
| 9.1 | 2, 4, 12, 18, 20, 22, 28, 30, 40, 44, 46, 48, 52, 58, 60 |
| 9.2 | 4. 8, 10, 12, 14, 18, 20, 24, 30, 32, 36, 40 |
| 9.5 | 2, 4, 10, 16, 18, 22, 32 |
| 9.6 | 2, 6, 12, 14, 16, 18, 22, 26, 40 |
| 9.7 | 2, 6, 10, 16, 18, 20, 22, 24 |
| 9.8 | 2, 4, 10, 14, 16, 18, 20, 24, 26, 28, 32, 34, 36, 38, 40, 46, 44, 48 |
| 9.9 | 2, 4, 6, 8, 10, 14, 18, 20, 22, 24, 26, 28, 34, 36, 38, 40, 42 |
MDS 123 Sample Exam
Answer all questions in the spaces provided. Use interval
notation where appropriate. Use
other correct notations where necessary and check your work whenever possible.
1. Suppose 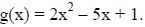 Simplify
Simplify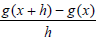
2. Given the piecewise function defined by
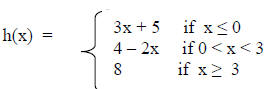
Find:
a) h(5),
b) h(-1)
c) h(2)
d) h(3)
e) h(0)
3. Write the domain of the each function in interval notation.
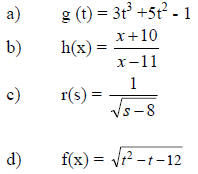
4. Complete the following table. Don’t approximate anything.
| x | 1/2 | 1 | 81 | ||
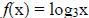 |
-2 | 5 |
5. Solve the following equations. Show your work in each
case. Give algebraic
solutions rather than graphical solutions. Leave your answers in exact form
(don’t
approximate).
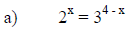
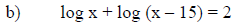
6. Suppose f is a linear function such that f (1) = 3.
Suppose also that g is the inverse
function for f and that g(4) = -2. Find the rule of f (x).
7. The table below shows the air temperature at various times during a spring
day in
Gainesville Florida
| Time | 6 a.m. | 8 a.m. | 10 a.m. | noon | 2 p.m. | 4 p.m. | 6 p.m. |
| Temp (°F) | 52 | 61 | 72 | 86 | 83 | 72 |
a) Determine the appropriate model ( linear , quadratic,
exponential, etc.) that
gives air temperature, y, as a function of time of day, x, with x = 0
corresponding to midnight. Use the regression capabilities of your
calculator to find the model to choose. If necessary, round coefficients to
three decimal places . What led you to choose the model you chose?
b) Using the mode you chose above, what is the predicted temperature at 10
p.m.
8. It has been suggested that brain cells perish in an exponential manner during
finals week. Suppose that at the beginning of the week Ann has 18 million
living brain cells, but after one day has passed he only has 17.6 million living
cells. Let x denote the number of days since the start of finals week, and let
f(x) denote the number of living brain cells (in millions) Ann has after x days.
For the following problems, give at 4 decimal places of accuracy.
a) write f(x) in the form f(x) = Pax
b) Write f(x) in the form f(x) = Pekx
9. The following statements are false, give a specific example that shows why
each statement is wrong.
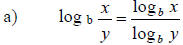
b) The graph of a quadratic function has at least one x- intercept .
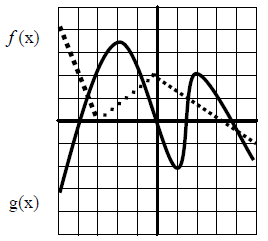
10.The graphs to the right completely
define two functions f and g. Assume
that gridlines mark one unit. Give
your best estimates when
appropriate. There are no arrows.
a) Give the intervals where
g (x) < f (x).
b) Compute (g o f )(-4)
c) Find the value (s) of x such
that g (x ) = 2
d) Give the interval(s) where
f (x) is increasing.
11. Perform the indicated operations:
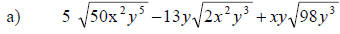
b) Subtract: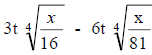
12. Solve the system using Cramer’s rule:
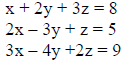
13. Solve: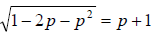
14. Simplify and write all answers as positive exponents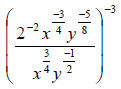
15. Simplify: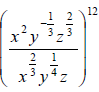
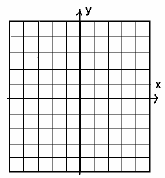
17. Sketch the graph of a function g that satisfies all of
the following conditions. Use
the grid provided to the right, and assume that gridlines mark one unit.
a) The domain of g is [-3, 5]
b) The range of g is [-2, 4]
c) g(x) is increasing only on the interval [-1, 0]
d) The average rate of change of g(x) between
x = -1 and x = 1 is 3/2
| Prev | Next |