Discrete Structures Homework Assignment 2 Solutions
Exercise 1 (10 points). Show that the sum of the first n odd natural numbers is n2.
Solution The proof is by induction. The induction
basis is trivial, the first odd natural
number is 1 so the sum is 1, and 12 = 1 of course. Now assume that the sum of
the first k
odd numbers is k2. The (k + 1)-st odd number is 2k + 1, and by the induction
hypothesis
the sum of the first k +1 odd numbers is k2 +2k+1. This is equal to (k +1)2
and the claim
thus holds for k + 1. This completes the proof.
Exercise 2 (10 points). What’s wrong with the following induction proof?
We prove that for any n ∈ N and any a ∈ R, an = 1. The
proof proceeds by
strong induction. For the induction basis, a0 = 1 and the claim holds. Assume
that the claim holds for all k up to n. Then
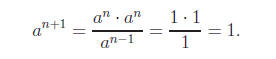
This proves the claim.
Solution In the very first induction step we are
assuming that the claim holds for n = 0
and need to prove correctness for n = 1. At that point the proof assumes that
the claim also
holds for n = −1, which was never proved and is not correct in general.
Exercise 3 (10 points). Prove by induction that,
for any set A, |2A| = 2|A|.
Solution The induction is on the cardinality. For the induction basis, any set
of cardinality
0 is the empty set; its power set is {ø}, so
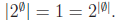 . Assume the claim holds for n = k,
. Assume the claim holds for n = k,
so for any set A such that |A| = k, |2A| = 2|A|. Any set A′ of k + 1 elements
can be seen as
a set A of k elements plus one new element e. A set S ∈ 2A′ either contains e
or not. Sets
that do not contain e are subsets of A and their number is 2|A| by the
induction hypothesis.
For a set S ∈ 2A′ that contains e, consider S0 = S \ {e}. S0 ∈ 2A and every
element of 2A
can be uniquely obtained in this way. Thus the number of sets S ∈ 2A′ that
contain e is also
2|A|. Together this implies that |2A′ | = 2×2|A| = 2|A|+1 = 2|A′|. This
concludes the induction
step and proves the claim.
Exercise 4 (10 points). Prove Bernoulli’s
inequality: For any n ∈ N and r ∈ R, such that
r > −1,
(1 + r)n ≥ 1 + rn.
Solution By induction on n. For the induction
basis, n = 0 and (1 + r)0 ≥ 1 + r0 since
1 ≥ 1. Assume that the claim holds for n = k, so (1 + r)k ≥ 1 + rk. We need to
prove the
inequality to k + 1. The induction hypothesis implies
(1 + r)k+1 ≥ (1 + rk)(1 + r) = 1 + rk + r + r2k ≥ 1 + rk + r = 1 + r(k + 1)
The first inequality follows from the assumption 1 + r ≥
0, which allows us to multiply the
inequality by 1 + r without changing the sign. The second inequality follows
since r2k ≥ 0.
This proves the induction step and concludes the proof.
Exercise 5 (10 points). Prove the strong induction
principle from the principle of induction.
Conclude that the two principles are equivalent. (That is, anything that can be
derived from
one, can also be derived from the other.)
Solution Given a set A of positive integers, assume
the conditions for the strong induction
principle:
• 1 ∈ A.  (1)
(1)
• If {1, 2, . . . , k} ⊆ A then k + 1 ∈ A.
 (2)
(2)
hold for the set A. We must show that A = N+, and we will do this by ordinary
induction.
Let P(n) be the following proposition:
“{1, 2, . . . , n} ⊆ A.”
For the base case, P(1) follows trivially from (1). Now
assume P(n) holds, and consider
P(n+1). From our induction hypothesis and (2), n+1 ∈ A, or in other words P(n)
implies
that {1, 2, . . . , n + 1} ⊆ A, which means P(n + 1)
is true. By the induction principle, P(n)
holds for all positive integers n, so N+ ⊆ A. But A
is a set of positive integers, so A = N+.
This proves the result.
The other direction (proving the induction principle from
the principle of strong induc-
tion) is similar but easier.
Exercise 6 (10 points). Suppose f(i, j) is a
function of i and j, and n ∈ N+. Prove or give
a counterexample:
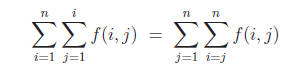
If the sums are replaced with products, does your conclusion change?
Solution They are indeed equal, as we’ll show by
induction on n. For the base case, n = 1
and both sides of the equation are f (1, 1), so they’re equal. Assume the claim
holds for
n = k. For n = k + 1, the left hand side is
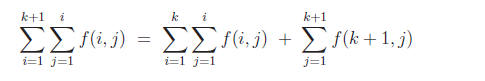
The last (single) sum is obtained by separating the case i = k + 1 from the
double sum.
Also, the right hand side is
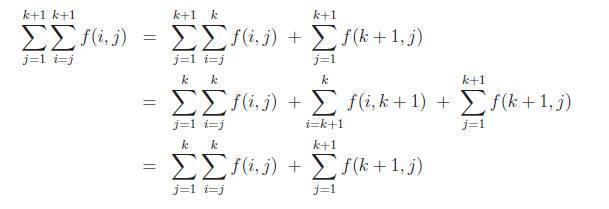
Note that the second sum in the second line evaluates to 0 because it has no
terms: the
starting value i = k + 1 is greater than the ending value i = k.
By our induction hypothesis,
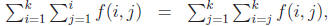 so the left and
so the left and
right hand sides are equal in the case n = k + 1 and the claim holds. This
proves the result
by induction.
If the sums are replaced with products, a completely
analogous proof is possible (we just
replace 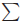 with
with
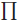 and + with ×). So the result holds in this
case too.
and + with ×). So the result holds in this
case too.
Exercise 7 (20 points). Many roots are irrational:
(a) Prove that 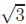 ,
,
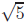 , and
, and 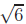 are
irrational. (Hint: For
are
irrational. (Hint: For 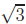 , use the fact that
every
, use the fact that
every
integer is of the form 3n, 3n + 1, or 3n + 2.) Why doesn’t the same proof
technique
imply that 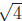 is irrational?
is irrational?
(b) Prove that 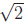 +
+
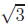 and
and 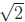 +
+
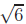 are irrational.
are irrational.
Solution
(a) Let’s start with the proof that 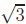 is
irrational. Following the proof that
is
irrational. Following the proof that 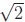 is
irrational
is
irrational
in the notes, we start by assuming 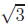 is
actually a rational number p/q, where p and q
is
actually a rational number p/q, where p and q
are integers with no common divisor and q ≠ 0, and show this leads to a
contradiction.
Squaring,
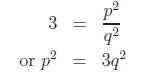
Now (from the hint) every integer is of the form 3n, 3n +
1 or 3n + 2, and the squares
in the three cases are 9n2, 9n2 + 6n + 1 and 9n2 + 12n + 4. The first is
divisible by
3 and the second and third leave a remainder of 1 when divided by 3. So a
perfect
square is a multiple of 3 if and only if its square root is divisible by 3. In
other words,
p must be divisible by 3, say p = 3k for some integer k. But then
9k2 = 3q2
or q2 = 3k2
and by the same argument, q must also be divisible by 3.
This contradicts our assump-
tion that p and q have no common divisor , and so
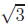 must, in fact, be irrational.
must, in fact, be irrational.
Identical proofs work for 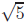 and
and
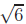 once we have proved that a number is
divisible
once we have proved that a number is
divisible
by 5 if and only if its square is divisible by 5, and likewise for 6.
This technique does not work for
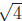 because an integer of the form 4n + 2 (which
is
because an integer of the form 4n + 2 (which
is
not divisible by 4) has the square 16n2 + 16n + 4 (which is divisible by 4). So
our
“if and only if” condition cannot be proved. Of course, we know that
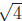 = 2 is very
= 2 is very
rational indeed.
(b) For 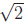 +
+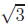 ,
we square to obtain
,
we square to obtain 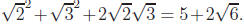 If this was a rational
If this was a rational
number p/q, we would have 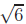 = (p − 5q)/2q,
which is a rational number. But we’ve
= (p − 5q)/2q,
which is a rational number. But we’ve
proved in the first part that 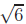 is irrational,
which proves the result by contradiction.
is irrational,
which proves the result by contradiction.
For 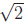 +
+ 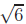 ,
the same method works , only we use the fact that
,
the same method works , only we use the fact that
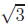 is irrational.
is irrational.
Exercise 8 (20 points). Consider n lines in the
plane so that no two are parallel and no
three intersect in a common point. What is the number of regions into which
these lines
partition the plane? Prove.
Solution The answer must be some function of n, which we’ll denote by F(n). We
can
consider putting down the lines one after the other on the plane (in any
arbitrary order ),
with the total number of regions increasing at each step. After putting the
first n − 1 lines
we have F(n − 1) regions. When we draw the nth line, we know it must intersect
all of the
other n−1 lines since no two lines are parallel. Since no three share an
intersection, this new
line has exactly n−1 intersection points with the other lines. These
intersections mean that
the new line goes through n of the existing regions of the plane (at every
intersection point,
the line leaves one existing region and enters another, and doesn’t change
regions before the
first intersection, after the last, or between any two intersections). The new
line divides each
region through which it passes into two, so n new regions are created. So
F(n) = F(n − 1) + n
It’s easy enough to expand this sum as:
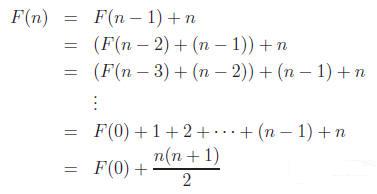
(recall the sum of the first n natural numbers)
Now when there are no lines, there is only one region (the
whole plane), so F(0) = 1. So
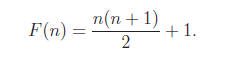
This, however, is not a formal proof! Rather, that was an
outline of the kind of reasoning
you could use to realize that the right answer is n(n + 1)/2 + 1. The actual
proof proceeds
by induction.
For the basis, with 0 lines there is 1 region so the claim
holds. Now assume it holds
for n = k. When we draw the (k + 1)-st line, we know it must intersect all of
the other
k lines since no lines are parallel. Since no three share an intersection, this
new line has
exactly k intersection points with the other lines. These intersections mean
that the new
line goes through k + 1 of the existing regions of the plane and divides each of
those in two,
such that k + 1 new regions are created. Adding this to the existing tally gives
a total of
k+1+k(k+1)/2+1 = (k2+3k+2)/2+1 = (k+1)(k+2)/2+1 = (k+1)((k+1)+1)/2+1
lines, so the claim holds for k + 1. This completes the proof by induction.
| Prev | Next |