Elementary Algebra Review
EQUATIONS AND INEQUALITIES
Simplifying Algebraic Expressions
Simplifying generally means creating equivalent expressions that contain fewer
additions and or
multiplications. To simplify algebraic expressions, combine like terms by adding
their coefficients and
keeping the variable parts the same. To simplify expressions containing
parentheses, remove all
parentheses and combine like terms . Remember to work problems containing
parentheses from the inner
most set outward.
| Example: |
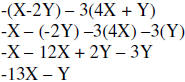 |
Distribute constants and signs |
| Perform all multiplications | ||
| Group like terms | ||
Solving Linear Equations
The solution to an equation is a number that, when substituted into the equation
for the variable, results in
a true equation. Solving the equation means finding all such numbers. The
general method of solving an
equation is to replace the given equation with simpler and simpler equations
until an equation of the form
variable=constant occurs. The constant is then called the solution of the
equation.
The two properties that are used to form these simpler equations are The
Additive Property of Equations
and The Multiplicative Property of Equations.
The Additive Property of Equations : Adding (or subtracting) the same quantity to
both sides of an
equation will not change the solution set of the equation.
| Example 1: | 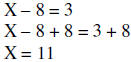 |
|
| Add 8 to both sides | ||
The Multiplicative Property of Equations: Multiplying (or
dividing) both sides of an equation by the same
nonzero number will not change the solution set of the equation.
| Example 2: | 5X = 27 | |
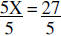 |
Divide both sides by 5 | |
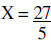 |
Anytime more than one property is used, always use the
addition property before the multiplication
property.
Example 3:
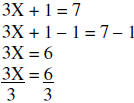
Solving Inequalities
An inequality states that one quantity is larger than another. The solution set
of an inequality is the set of
all numbers that make the inequality true when substituted into the original
inequality. These solution
sets are found using similar properties as those used to solve equations.
| Example: | 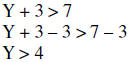 |
|
| Subtract 3 from both sides | ||
| Graph the solution set |
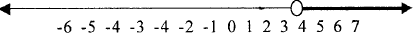
The Multiplicative Property of Inequalities: Multiplying
(or dividing) both sides of an inequality by the
same positive non -zero number will not change the solution set of the
inequality. Multiplying (or
dividing) both sides of an inequality by the same non-zero negative number
reversing the inequality does
not change the solution set of the inequality.
| Example 2: | 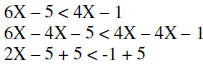 |
|
| Subtract 4X | ||
| Add 5 | ||
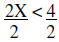 |
Divide by positive 2 | |
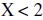 |
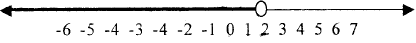
| Example 3: | 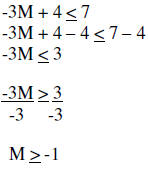 |
|
| Subtract 4 | ||
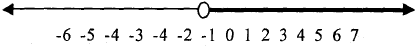
Exercises
Simplify each of the following
1. -3V + 7V – V
2. 12X – 3Y + 5X + 5Y
3. -7M + 9(2M – 3)
4. –(2X – 7Y) – 3(2Y – 11X)
5. 3[2X – 3(X – 2Y)] + 3Y
Solve each of the following Equations

11. Solve for X: (3X + Y) – (Y-X) = 5 (2X + Y)
12. The sum of two numbers is 18. The difference between four times the smaller
number and seven is
equal to the sum of two times the larger number and five. Find the two numbers.
13. Jane bought a television set at a 20% off sale. If she paid $360 for the
set, what was the original price.
14. How many gallons of water must be mixed with 5 gal of 20% salt solution to
make a 16% salt
solution?
15. The perimeter of a triangle is 23ft. One side is twice the second side. The
third side is 3ft. more than
the second side. Find the measurements of each side.
Solve the following inequalities. Graph your results.
16. 2X < 6X – 8
17. 13 – 4X < X – 2
18. 4X + 9 > X – 7
19. Two sides of a triangle must be 8m and 12m. The perimeter must be at least
24m at most 39m.
Determine the length that can be used for the third side.
20. An insurance company is developing a new policy that is expected to have an
average annual claim of
at least $409. The yearly premium for the policy will be $390. To make up the
underwriting loss the
company plans to put the premium money into an investment that is expected to
yield an annual profit of
between 4.3% and 4.8% after other expenses are covered. Under these conditions,
will this policy make
money for the company?
EXPONENTS AND POLYNOMIALS
Integer Exponents
The following properties are used to work with exponents.
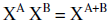 |
To multiply with the same base you add exponents |
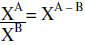 |
To divide with the same base you subtract exponents |
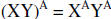 |
Exponents distribute over multiplication |
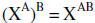 |
A power to a power is the product of the powers |
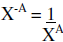 |
Negative exponents imply reciprocals |
| Example 1: | 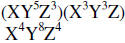 |
Add exponents for like bases |
| Example 2: | 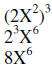 |
Multiple Exponents |
| Example 3: | 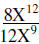 |
|
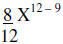 |
Divide the numerical coefficients Subtracts the exponents on the variables |
|
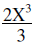 |
Simplify | |
| Example 4: | 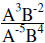 |
|
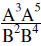 |
Make all exponents positive | |
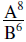 |
Add exponents for the like bases |
| Prev | Next |