Elementary Algebra Review

Exercises
Reduce each rational expression to lowest terms

Perform the indicated operations

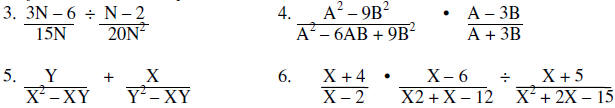
Solve each of the following equations.

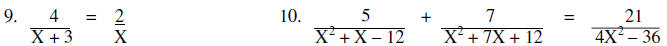
11. The speed of the current in a river is 5mph. If a boat can travel 198 miles with the current in the same
time it could travel 138 miles against the current, what is the speed of the boat in still water?

12. An inlet pipe can fill a tank in 10 minutes. A drain can empty the tank in 12 minutes. If the tank is
empty and both the pipe and the drain are open, how long will it take before the tank overflows?

13. Connie can type 600 words in 5 minutes less than it takes Katie to type 600 words. If Connie can
type at a rate of 20 words per minute faster than Katie types, find Connie’s typing rate.

14. The ratio of the squares to two consecutive even integers is 9/16. Find these integers.

ROOTS AND RADICALS

Simplifying Radical Expressions

Radical expressions are algebraic expressions which contain a radical. A radical expression is simplified
when the radicand (expression under the radical) does not contain any powers greater than or equal to the
index, there are no radicals in the denominator and all fractions are in the lowest terms.

Example: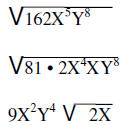
		Write factors as perfect squares if possible
		Remove the squares

Adding and Subtracting Radical Expressions

Adding and Subtracting can be done on terms with like radical portions. When the terms have like racial
parts, add or subtract in the same manner as when adding or subtracting like terms.

Example: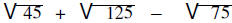
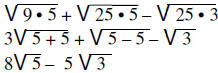		Write as product of squares
		Remove squares
		Combine like terms

Multiplying and Dividing Radical Expressions

Radical expressions are multiplied in the same way as other expressions. Coefficients are multiplied
together and stay coefficients; radicands are multiplied together and remain radicands .The result is then
simplified.

Example: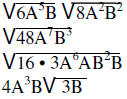
		Multiply
		Simplify
Example: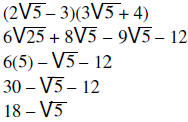
		FOIL
		Simplify
		Combine like terms

To divide one radical expression by another, write the division as a fraction and simplify.

Example: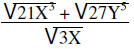
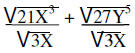		Write each division separately
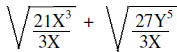		Write as one radical
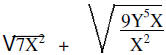		Simplify

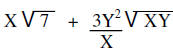To simplify a fraction that has a binomial radical expression in the denominator, multiply the numerator
and denominator by the conjugate form of the denominator and simplify.

Example: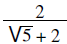
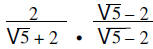		Multiply by the conjugate

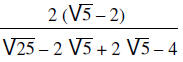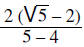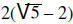Solving Equations with Radical Expressions

Equations that contain radicals can be solved by using the equality property of powers, which states that if
two real numbers are equal, then any natural power of these numbers is also equal. To use this property,
first isolate the radical on one side of the equation. Next raise both sides of the equation to the same
power and solve as usual. Always check all answers to eliminate “imposter roots” that may be introduced
by the squaring process.

Example: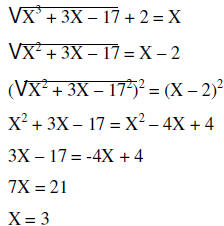
		Isolate the radical
		Square both sides
		FOIL
		Subtract X2 from both sides
		Combine like terms
		Divide by 7
Example: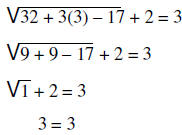
		The root is true

Exercises

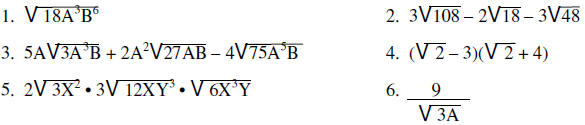
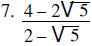
Solve each of the following:

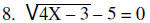
9. An object is dropped from an airplane. Find the distance the object has fallen when the speed reaches
400 feet per second. Use the equation 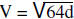, where V is the speed of the object and d is the distance.

10. How fare would a submarine periscope have to be above water to locate a ship 4.2 miles away? The
equation of the distance in miles that the lookout can see is 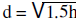, where the height in feet above the
surface of the water and distance.

11. Find the width of a rectangle that has a diagonal of 10 feet if the length is 2 feet longer than the width.

12. When trying to put out a fire, fire fighters are interested in the flow rate of the water available at the
site of the fire. The flow rate is determined by the equation 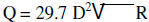where Q is flow rate in
gallons per minute, d is diameter of the hose nozzle in inches and P is static pressure in pounds per inch.
What is the minimum static pressure to get at least 594 gal /min from a 2in fire hose?