Exponential Growth and Decay & Linear Equations
Problem 1
A bacteria culture starts with 1000 bacteria and the growth rate is proportional
to the
number of bacteria . After 2 hours the population is 9000.
(a) Find an expression for the number of bacteria after t hours.
(b) Find the number of bacteria after 3 hours.
(c) Find the rate of growth after 3 hours.
(d) How long does it take for the number of bacteria to double?
Problem 2
Carbon-14 dating is a technique used to determine the age of various objects.
All plants
and animals have the same ratio of Carbon -14 to Carbon-12 while they’re alive.
When they
die, the Carbon-14 begins to decay but the amount of Carbon-12 remains constant.
By using
the half life of Carbon-14 scientists can deduce the age of the object in
question.
(a) While it was alive, a plant contained .64 mg of Carbon 14. The plant died
22,800 years
ago and now contains .16 mg of Carbon 14. What is the half life of Carbon 14?
(b) Your friend gives you a bone which she says once belonged to a Tyrannasaurus
Rex,
a dinosaur that lived over 65 million years ago. The amount of Carbon-14 in the
bone is .05
mg. Assuming the animal had .64 mg of Carbon-14 in its bones when it died,
should you
believe your friend?
Problem 3
Solve the following differential equations .
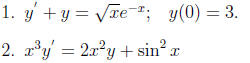
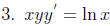
Problem 4
Consider the differential equation
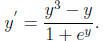
1. Find all its constant solutions .
2. Discuss
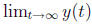 ,
where y(t) is the solution such that
,
where y(t) is the solution such that
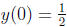 .
.
Problem 5
Let n be an integer larger than 1. Is there a differentiable function on [0,∞)
whose derivative
equals its nth power and whose value at the origin is positive?
| Prev | Next |