Foundations of Mathematics
Making a Statement
In order to do any kind of mathematics, we need to be able
to determine the truth or falsity of
validly formed mathematical statements . Let’s spend today investigating these
ideas, introducing
the notion of quantifiers along the way.
• A (valid) mathematical statement is any “grammatically
correct” assertion to which we can
assign one of the two truth values TRUE or FALSE.
Examples. You might want to indicate the truth
value of each statement beside it!
(1) 1 + 1 = 4
(2) There is a number x greater than any real number.
(3) π is a rational number .
(4)
(5)
(6)
• Sometimes the truth value of a statement is incalculable
without further specifying the
values of quantities contained in the statement. For example, the statement “x^2
> 1”
might be true or it might not be, depending on what value the variable x has .
There are
two common ways of quantifying a variable in a statement:
(1) The variable x in a mathematical statement is
universally quantified in the statement
“For all x in the set S, property P (x) about the variable x holds.” You should
be able
to identify S, P(x), and the truth value of the statement, in each case below.
Examples.
(a) x^2≥0 for all real numbers x.
(b) For every integer x, x < 97.
(c)
(d)
(2) The variable x is existentially quantified in the
statement “There exists x in the set S
such that the property P(x) holds.”
Examples.
(a) For some rational number x , x is larger than π.
(b) There exists a circle in the Cartesian plane bounding an area larger than 1
square unit.
(c)
(d)
The set S of allowed values for a variable x is called its universe.
• Quantifiers arise so often that we seek special notation
for them:
– Universal quantifiers are written (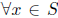 ) P(x).
You should translate the first two
) P(x).
You should translate the first two
universal statements above using this notation:
(1)
(2)
– Existential quantifiers are written (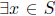 ) P(x).
Translate the first two existential
) P(x).
Translate the first two existential
statements given above:
(1)
(2)
• Many statements are formed by combining quantifiers .
When more than one quantifier appears,
it’s important to understand the order of quantification, as indicated in the
following
examples:
Examples.
(1) “For every real number a there exists a real number b such that a < b” means
something
other than...
(2) ...“There exists a real number b such that for every real number a, a < b.”
(You
should be able to translate these into our new notation and note the difference
between
the two!) Now write your own pair of statements where the order makes all of the
difference:
(3)
(4)
• New statements can be formed from old ones by negation.
To negate a statement is to
reverse its truth value. You should be able to negate the following statements,
and then
invent a couple of your own to negate:
(1) There is a real number x such that x + 6 = 7.
(2) For every integer z, z > 0.
(3)
(4)
Below, translate each of the above statements, and their
negations, into our notation for
quantifiers (I’ve done the second one for you):
(1)
(2) 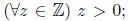 negation:
negation:
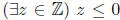 . (Note that “not z > 0” is the same as
. (Note that “not z > 0” is the same as
“z≤0.”)
(3)
(4)
By the way, the negation of a statement P(x) is generally
written ¬P(x). From the
above examples, can you formulate a rule which allows you to negate a statement
with
quantifiers, replacing it with a new statement without a “¬” out in front? Fill
in your
conjecture below:
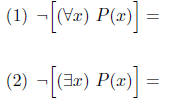
Example. Test your conjecture by negating the
following statement using your rule,
after translating it into our quantifier notation: “For every integer a there
exists a real
number b such that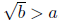 "
"
| Prev | Next |