INTERMEDIATE ALGEBRA
COURSE DESCRIPTION: This course is designed to assist students making a transition from elementary mathematics to calculus. The topics include a review of exponents, factoring, linear and quadratic equations, inequalities, functions, graphs, system of equations, exponential and logarithmic functions.
PREREQUISITE: MATH 105 (with a grade of C or better) or Placement Test
COREQUISITE: None
STUDENT RESPONSIBILITIES:
1. The student should pre-study (read) all new topics before the topics are
presented in class. The student is expected to complete daily homework
assignments before the next class starts. Students are required to get the home
assignment checked within a week from the day it is assigned by coming during
office hours. The instructor will ascertain the daily progress in accomplishing
homework exercises and will devote a portion of classroom activities to the
solutions of any troublesome exercises.
2. Students are required to maintain a separate notebook for this course, and
all work related to this course must be done in this notebook. They must bring
this notebook to every class. Students are expected to devote a minimum of 10
hours per week outside the class. Each student must use a scientific calculator
when necessary.
3. Students are strongly encouraged to participate in classroom discussions.
4. Tests will be administered during the course; a mandatory, departmental,
comprehensive final examination will also be given. Students must complete
the online lab tests and earn a minimum of 70% on each to become eligible to
take the in-class test. A score of less than 70% will not earn any credit. All
students must take all lab tests, in-class tests, and the final examination when
scheduled.
NOTE: Any student who does not show up by the third week of classes will be
deleted from the roster.
COURSE RATIONALE: It is a required course primarily for non-science majors. The material covers application of mathematics in business. A pre-requisite course for MAT-132 Calculus for non-science majors is needed.
COURSE GOALS and MEASURABLE INTENDED STUDENT LEARNING OUTCOMES:
Goals: By attending the lectures, completing the assignments, and
participating in class, the student should accomplish the following objectives:
• Understand algebraic concepts on a pre-calculus level.
• Analyze and solve problems involving business applications.
• Demonstrate the ability to manipulate formulas and evaluate them on a
calculator.
• Realize that algebra is a tool used in higher mathematics.
Measurable Outcomes: Upon completion of the course, the student should
have at least level of proficiency of 70% and should be able to:
• Apply the laws of positive and negative integral exponents, the zero-exponent,
rational exponents, principal roots, and radicals.
• Rationalize the denominator , and factor expressions completely.
• Discuss equivalent equations and develop techniques for solving linear and
literal equations.
• Solve fractional and radical equations.
• Solve quadratic equations by factoring or by using the quadratic formula.
• Model situations described by linear and quadratic equations (business
applications).
• Solve linear inequalities with one variable and introduce interval notation.
• Model situations in terms of inequalities (business applications).
• Solve equations and inequalities involving absolute values.
• Understand what a function is and determine domains and function values.
• Recognize constant functions, polynomial functions , rational functions,
compound functions, the absolute value function, and factorial notation.
• Combine functions by means of addition, subtraction , multiplication, division,
and composition.
• Graph equations and functions in rectangular coordinates, determine
intercepts, apply the vertical-line test, and determine the domain and range of
a function from a graph.
• Know the shapes of six basic functions and to consider translation and
reflection of the graph of a function.
• Develop the notion of slope and different forms of equations of lines.
• Understand the notion of demand and supply curves and linear functions.
• Sketch parabolas arising from quadratic functions.
• Solve systems of linear equations in two variables by using the technique of
elimination or by substitution.
• Solve nonlinear systems of equations.
• Solve systems describing equilibrium and break-even points.
• Understand exponential functions and their applications to the area of
compound interest.
• Understand logarithmic functions and their graphs.
• Understand the basic properties of logarithmic functions.
• Solve logarithmic and exponential equations.
COURSE MATERIALS/ REQUIRED TEXT / SUPPLEMENTARY READINGS
Text: Applied Mathematics for the Managerial, Life, and Social Sciences, 4th
Edition
by Tan
ISBN #0-495-01581-4
PRIMARY METHOD OF INSTRUCTION/METHODS TO ENGAGE STUDENTS: The content of the course is covered in an in-class room lecture setting. Each lecture class covers the theory and related problems from the exercise. For in depth understanding of subject in-class discussions are encouraged. Students are required to solve enough number of problems until they are comfortable with the methods/techniques introduced in the class. It is mandatory to complete the related lab assignment as per calendar supplied with this document. Any difficulties are discussed on one-to-one basis during the office hours. Evaluations are done after sufficient materials are covered, and the graded evaluations are returned to them as a feed back of their performances. Students are required to maintain separate notebook for this course and all work related to this course must be done in this notebook. They must bring this notebook to every meeting – lecture/tutorial or help sessions. Students are expected to devote a minimum of 7 hours per week outside the class.
COURSE OUTLINE/ CALENDAR (Detailed course calendar is attached)
| Review | Section 1.1 – Real Numbers | 2 |
| Section 1.2 – Polynomials | 7 | |
| Chapter 1 | Fundamentals of Algebra | |
| Section 1.3 – Factoring Polynomials | 15 | |
| Section 1.4 – Rational Expressions | 21 | |
| Section 1.5 – Integral Exponents | 27 | |
| Section 1.6 – Solving Equations | 32 | |
| Section 1.7 – Rational Exponents and Radicals | 38 | |
| Section 1.8 – Quadratic Equations | 46 | |
| Section 1.9 – Inequalities and Absolute Value | 56 | |
| Chapter 2 | Functions and Their Graphs | |
| Section 2.1 – The Cartesian Coordinate System and Straight Lines | 72 | |
| Section 2.2 – Equations of Lines | 78 | |
| Section 2.3 – Functions and Their Graphs | 92 | |
| Section 2.4 – The Algebra of Functions | 108 | |
| Section 2.5 – Linear Functions | 117 | |
| Section 2.6 – Quadratic Functions | 129 | |
| Section 2.7 – Functions and Mathematic Models | 140 | |
| Chapter 3 | Functions and Graphs | |
| Section 3.1 – Exponential Functions | 160 | |
| Section 3.2 – Logarithmic Functions | 167 | |
| Section 3.3 – Exponential Functions as Mathematical Models (Exp. Decay) | 177 | |
| Chapter 4 | Exponential and Logarithmic Functions | |
| Section 4.1 – Compound Interest | 192 | |
| Chapter 5 | Systems of Linear Equations | |
| Section 5.1 – Systems of Linear Equations: An Introduction | 252 | |
| Chapter 6 | Linear Programming | |
| Section 6.1 – Graphing Systems of Linear Inequalities in Two Variables | 338 |
RELATED UNIVERSITY-WIDE AND COURSE-SPECIFIC REQUIREMENTS:
• Writing: The assessments in this course will include open ended
questions to encourage students to master the writing ability in mathematics.
• Information Technology Literacy: The student will explore various
websites to gain a better understanding of math concepts and problems. The
student is also required to do math labs online. Students are encouraged to
communicate (outside of the class) with the professor or classmates through
electronic means.
• Quantitative Reasoning: Most of the math concepts have applications
that require quantitative reasoning.
• Scientific Reasoning: Most of the math applications require the use of
scientific reasoning.
• Oral Communication: The student demonstrates oral communication through
classroom discussions and explanations at the board.
• Critical Thinking: Most of the math concepts and applications require
critical thinking.
• Other Requirements: The student is required to do the iLrn assignments
homework and lab tests for the course.
EVALUATION/ ASSESSMENT METHOD: Students learning evaluations will be done throughout the session at regular interval. Evaluations will include eight lab tests, four in-class tests, homework, pop-quizzes, and a comprehensive common final examination (compulsory). In case of missed test(s) due to excused absences, the final examination will accordingly be prorated. The tests and examinations will be conducted as per following schedule:
| Lab Test I: Sept. 10, 2007 | Lab Test II: Sept. 16, 2007 | In-class Test I: Sept. 17, 2007 |
| Lab Test III: Oct. 3, 2007 | Lab Test IV: Oct. 9, 2007 | In-class Test II: Oct. 10, 2007 |
| Lab Test V: Oct. 29, 2007 | Lab Test VI: Nov. 4, 2007 | In-class Test III: Nov. 5, 2007 |
| Lab Test VII: Nov. 21, 2007 | Lab Test VIII: Nov. 27, 2007 | In-class Test IV: Nov. 28, 2007 |
GRADING STANDARDS / EVALUATION CRITERIA:
Mid-Term Grade:
Average of four lab tests, Test I, and Test II will determine the mid-term grade.
Final Grade:
| Four In-Class Tests | 4 × 25 = 100 points |
| Eight Lab Tests | 8 × 4 = 32 points |
| Homework and Pop Quizzes | = 28 points |
| Final Examination | = 40 points |
|
200 points |
FINAL EXAM: Thursday, December 7, 2007 10:30 AM – 12:30 PM
COURSE GRADE EVALUATION: The following grades are guaranteed if you earn the corresponding percentage of the total points by the end of the semester:
| 59 &below | 60-69 | 70-79 | 80-89 | 90 &above |
| F | D | C | B | A |
ACADEMIC INTEGRATY STANDARDS: Further information regarding academic-related conduct, disciplinary procedures, honesty, honor code, violation of integrity (such as plagiarism) and sanctions regarding such misconduct may be obtained by consulting the NSU Student Handbook.
Attendance Policy: Students are expected to attend each class. Attendance will be taken daily. If tardy, please notify the instructor at the end of the class period. Any absence from class doesn’t relieve any student of the responsibility for completing all class work and assignments. With satisfactory explanation, an absence may be considered excused. In general, an excused absence will include any kind of illness, participation in university-sponsored activities, recognized emergencies, etc., verified and supported by a written statement from the proper authority. Missing 20% or more of such sessions may result in an automatic failing grade. Those individuals who choose not to show up for class by the end of the third week will be deleted from the roster.
Cell Phone Usage: Students are reminded to turn the ringer off during any formal meeting of the course including class, tutorial, tests, and examination.
TECHNOLOGY REQUIREMENTS: Students are expected to be familiar with usage of TI-83-Plus graphing calculator or a calculator with equivalent capabilities.
AMERICANS WITH DISABILITIES ACT (ADA) STATEMENT: In accordance with Section 504 of the 1973 Rehabilitation Act and the Americans with Disabilities Act (ADA) of 1990, we ask if you have a disability, please call Ms. Marian E. Sheppard, coordinator at 823-2014 or make contact with the Supporting Students through Disability Services (SSDS) office located in Rm. 240 (2nd Floor)-Assistive Technology Lab, Lyman Beecher Brooks Library.
ACADEMIC SUPPORT SERVICES: Students are encouraged to take advantage of on campus testing and tutoring services. They can use the computers in STARS and ACCESS labs to complete their iLrn home assignments and online labs.
UNIVERSITY ASSESSMENT STATEMENT: As part of NSU’s commitment to provide the environment and resources needed for success, student may be required to participate in a number of university-wide assessment activities. The activities may include tests, surveys, focus groups and interviews, and portfolio reviews. The primary purpose of the assessment activities is to determine the extent to which the university’s programs and services maintain a high level of quality and meet the needs of the students. Students will not be identified in the analysis of results. Unless indicated otherwise by the instructor, results from University assessment activities will not be computed in the student grades.
OTHER IMPORTANT DATES:
| Aug. 18, 2007: | Classes Begin/Late Registration |
| Sept. 3, 2007: | Labor Day Holiday (No Classes) |
| Sept. 6, 2007: | Fall Convocation |
| Oct. 1 – Oct. 6, 2007: | Mid-Semester Advisory Exam Period |
| Oct. 12, 2007: | Last Day to Drop a Course |
| Nov. 22 – Nov. 25, 2007: | Thanksgiving Break |
| Nov. 30, 2007: | Classes End |
FALL 2007 MATH-131 (Pre-Calculus for Non-Science Major) - MWF
TEXT: Applied Mathematics for the Managerial, Life, and Social Sciences,
4th Edition by Tan
Laboratory Tests
Course Key: E-EZX527GJUYYN
| Lab Test | Contents | Due Date |
| 1 | Real Number, Polynomials, Factoring Polynomials, Rational Expressions | Sept. 10, 07 |
| 2 | Integral Exponents, Solving Equations, Rational Exponents, Radicals | Sept. 16, 07 |
|
IN-CLASS TEST I: Sept. 17, 2007 |
||
| 3 | Quadratic Equations, Inequalities, Absolute Value | Oct. 3, 07 |
| 4 | The Cartesian Coordinate System and Straight Lines, Equations of Lines | Oct. 9, 07 |
|
IN-CLASS TEST II: Oct. 10, 2007 |
||
| 5 | Functions and Their Graphs, The Algebra of Functions, Linear Functions, Quadratic Functions | Oct. 29, 07 |
| 6 | Functions and Mathematical Models, Exponential Functions, Logarithmic Function | Nov. 4, 07 |
|
IN-CLASS TEST III: Nov. 5, 2007 |
||
| 7 | Exponential Functions as Mathematical Models, Compound Interest | Nov. 21, 07 |
| 8 | Systems of Linear Equations: An Introduction, Unique Solution, Graphing Systems of Linear Inequalities in Two Variables | Nov. 27, 07 |
|
IN-CLASS TEST IV: Nov. 28, 2007 |
||
8 Lab Tests: 16% 4
In-Class Tests: 50%,
Homework/ Pop Quizzes: 14%
Final Exam: 20%
MATH 131
Flowchart
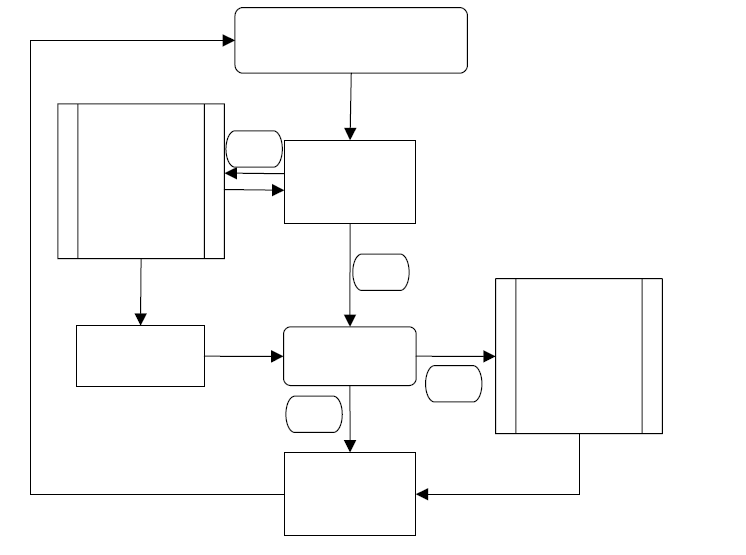
** No Credit Awarded for Lab Tests not
passed.
Lab Tests count for 16% of Final Grade.
Math 131: FALL 2007 Calendar**
| Wk | Day | Date | Topics | Notes | ||
| 1 | 1 | M | 8/20 | 1.1&1.2 | Real Numbers & Polynomials | |
| 2 | W | 8/22 | Diagnostic Test | |||
| 3 | F | 8/24 | 1.3 | Factoring Polynomials | ||
| 2 | 4 | M | 8/27 | 1.4 | Rational Expressions | |
| 5 | W | 8/29 | 1.4 | Integral Exponents | ||
| 6 | F | 8/31 | 1.5 | Solving Equations | ||
| 3 | -- | M | 9/3 | 1.6 | Labor Day Holiday | |
| 7 | W | 9/5 | 1.7 | Rational Exponents | ||
| 8 | F | 9/7 | 1.7 | Radicals | ||
| 4 | 9 | M | 9/10 | 1.8 | Quadratic Equations | Lab Test I Due |
| 10 | W | 9/12 | 1.9 | Inequalities & Absolute Value | ||
| 11 | F | 9/14 | 1.3 - 1.9 | Cumulative ReviewTest-1 | Lab Test II Due (9/16) | |
| 5 | 12 | M | 9/17 | 1.3 - 1.9 | Test-1 | IN-CLASS TEST I |
| 13 | W | 9/19 | 2.1 | The Cartesian Coordinate System and Straight Lines | ||
| 14 | F | 9/21 | 2.1 | The Cartesian Coordinate System and Straight Lines | ||
| 6 | 15 | M | 9/24 | 2.2 | Equations of Lines | |
| 16 | W | 9/26 | 2.3 | Functions and Their Graphs | ||
| 17 | F | 9/28 | 2.4 | The Algebra of Functions | ||
| 7 | 18 | M | 10/1 | 2.5 | Linear Functions | |
| 19 | W | 10/3 | 2.6 | Quadratic Functions | Lab Test III Due | |
| 20 | F | 10/5 | 2.7 | Functions and Mathematical Models | ||
| 8 | 21 | M | 10/8 | 2.1-2.7 | Cumulative Review | Lab Test IV Due (10/9) |
| 22 | W | 10/10 | 2.1-2.7 | Test-2 | IN-CLASS TEST II | |
| 23 | F | 10/12 | REV | Cumulative Review | ||
| 9 | 24 | M | 10/15 | 3.1 | Exponential Functions | |
| 25 | W | 10/17 | 3.1 | Exponential Functions | ||
| 26 | F | 10/19 | 3.2 | Logarithmic Functions | ||
| 10 | 27 | M | 10/22 | 3.2 | Logarithmic Functions | |
| 28 | W | 10/24 | 3.3 | Exponential Functions as Mathematical Models | ||
| 29 | F | 10/26 | 3.3 | Exponential Functions as Mathematical Models | ||
| 11 | 30 | M | 10/29 | 3.1-3.3 | Cumulative Review | Lab Test V Due |
| 31 | W | 10/31 | 4.1 | Compound Interest | ||
| 32 | F | 11/2 | 3.1-4.1 | Cumulative Review | Lab Test VI Due (11/4) | |
| 12 | 33 | M | 11/5 | 3.1-4.1 | Test-3 | IN-CLASS TEST III |
| 34 | W | 11/7 | 5.1 | Systems of Linear Equations: An Introduction | ||
| 35 | F | 11/9 | 5.1 | Systems of Linear Equations: An Introduction | ||
| 13 | 36 | M | 11/12 | 5.1 | Review | |
| 37 | W | 11/14 | 6.1 | Graphing Systems of Linear Inequalities in 2-Variables | ||
| 38 | F | 11/16 | 6.1 | Graphing Systems of Linear Inequalities in 2-Variables | ||
| 14 | 39 | M | 11/19 | 5.1-6.1 | Review | |
| 40 | W | 11/21 | 5.1-6.1 | Review | Lab Test VII Due | |
| -- | F | 11/23 | Thanksgiving Holiday | |||
| 15 | 41 | M | 11/26 | QA | Question & Answer Session, Make-ups, and Reviews | Lab Test VIII Due (11/27) |
| 42 | W | 11/28 | Test-4 | IN-CLASS TEST IV | ||
| 43 | F | 11/30 | QA | Question & Answer Session, Make-ups, and Reviews | ||
** This schedule is subject to change at the discretion of the Instructor depending upon progress of the class.
| Prev | Next |