Math 120 Review Final Exam
1. Give two examples of
(a) An integer that is not a natural number.
-5,-3, , 2 (any negative integer )
(b) A rational number that is not an integer.
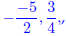 (any quotient of whole numbers with
denominator not one )
(any quotient of whole numbers with
denominator not one )
(c) A real number that is not a rational number.
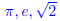
2. Solve the following equations

3. Solve the following inequalities. give your answer in interval notation:

4. The diameter of a circle is the segment with endpoints
(-2, 2) and (4,-4). Find the equation of
this circle .
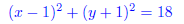
5. Find the radius and center of the following circles:
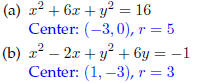
6. Show the points (-2,-2), (3, 3) and (4, 0) form a right triangle.
(a) By computing the slopes of the sides.
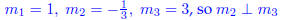
(b) By using the distance formula .
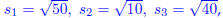 so the pythagorean
theorem is satisfied:
so the pythagorean
theorem is satisfied:
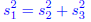
7. Find the equation of the line that goes through the point (-2, 1) and is
(a) parallel to the line 2x - 3y = 5
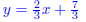
(b) perpendicular to the line 2x - 3y = 5
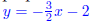
8. Find the average rate of change for the following functions in the given interval
(a) f(x) = 3x^2 - 3 on the interval [-1, 1] 0
(b) f(x) = 3x^2 - 3 on the interval [-1, 0] -3
(c) f(x) = 3x^2 - 3 on the interval [0, 1] 3
9. Find the difference quotient for the following functions and simplify :

10. Given f(x) = x + 2 and g(x) = 4 - x^2 find the following:

11. Find the inverse of each of the following functions.
Verify that you found the inverse by checking
that 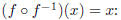

12. Use transformation on a basic function to sketch the
graph of the following functions. State which
is your basic function and describe the sequence of transformations you
performed in order to
obtain your graph.
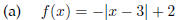
Basic fcn: F(x) = |x|
moved 3 units to the right
reflected over the x-axis
shifted 2 units upward
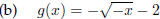
Basic fcn: 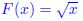
reflected over the y axis
reflected over the x axis
shifted 2 units downward
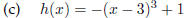
Basic fcn: F(x) = x^3
shifted 3 units to the right
reflected over the x-axis
shifted 1 unit up
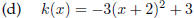
Basic fcn: F(x) = x^2
shifted 2 units left
stretched horizontally by a factor of 3
shifted 3 units upward
13. The functions f and g are given by the following tables:

(a) Find (f + g)(2) = 3
(b) Find the domain of f/g = {2}
(c) Find 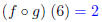
(d) Find the domain of 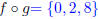
14. A local peanut butter manufacturer has a daily production costs of
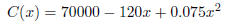
where x is the number of units produced and C(x) is the
cost in dollars. How many units should
be produced each day to yield minimal cost?
160
15. Find two quadratic functions , one that opens upward,
one that opens downward, whose graphs
have the given x-intercept:
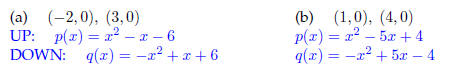
16. Find all the real zeroes of the following functions:
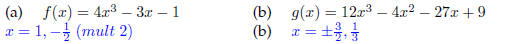
17. Find a polynomial equation with real coefficients that
has roots 1 - i, 3, and 1.(if 1 - iis a root,
then 1 + i is a root also, so you multiply (x - (1 - i))(x - (1 + i))(x - 3)(x -
1)and get
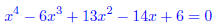
18. Find a polynomial equation with real coefficients that
has 2 as a zero of multiplicity 2 and -2 as a
zero of multiplicity one .
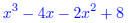
19. Perform the following operations and write your answer in standard form.
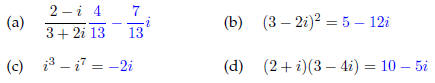
20. Solve the following equations:
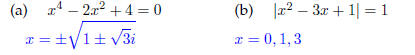
21. Knowing that -1 - 3i is a zero of the polynomial
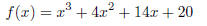
find the complete factorization of f(x)
(x + (1 - 3i)) (x + (1 + 3i)) (x + 2)
22. Find a polynomial of degree 4 with real coefficients that has -1, 1 and 2i as zeroes.
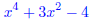
23. Of all possible rectangles with perimeter equal to 200
ft, find the dimensions of the one with
maximum area. its a square with 50 ft on each side
24. Use either long division, or synthetic division to
verify that (x - 4) and (x + 2) are factor of the
polynomial
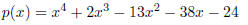
Then factor the polynomial completely.
(x - 4)(x + 1)(x + 2)(x + 3)
25. Solve the following inequalities
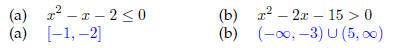
26. Find the exact value of cos θ for an angle θ in
standard position whose terminal side contains the
point (1,-4).
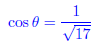
27. From a point on the bank of a stream to the top of a
50 ft high cliff, directly across the stream, the
angle of elevation is 73º.
How wide is the stream?
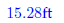
28. Find the exact value of each expression :

29. The radius of the earth is approximately 3950 miles.
Find the distance over the surface of the earth
from the North Pole to the South Pole.
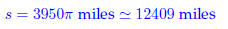
30. An airplane, flying at an altitude of 6 miles, is on a flight path that passes directly over you. If θ is the angle of elevation from you to the plane, find the distance between you and the plane when
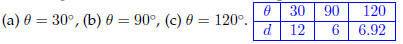
31. A Ferris wheel is built such that the height h, in
feet, above the ground of a seat on the wheel at
time t (in seconds) can be modeled by the function
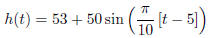
(a) Find the period of this function. What does the period
tell you about the ride?
P = 20, The ride takes 20 seconds in complete one full cycle.
(b) Find the amplitude of the model. What does the amplitude tell you about the
ride?
A = 50, the distance between the highest and the lowest point in the ride is
2A = 100 ft.
32. A safety regulation state that the maximum angle of
elevation for a rescue ladder is 72º.
A fire
department’s longest ladder is 110 ft long. What is the maximum safe rescue
height?
33. Verify the following identities:


34. Find the exact value of the following expressions
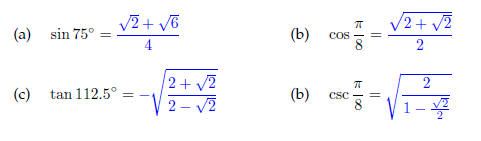
| Prev | Next |