Math 134: Review Worksheet
Calculus draws on essentially everything you have learned to this point in
math . The goal of
this worksheet is to reacquaint you with some of the more important concepts
involving algebra
and functions that we will be using.
The following problems range from very easy to fairly difficult (in no
particular order). You
should feel free to use whatever resources you want to solve these problems. You
are welcome to
work together, use your calculator , refer to the book, et cetera. If you get
stuck on a problem,
move on and come back to it.
That being said, this worksheet is not meant to be busy work. For each set of
problems,
reflect on your answers and decide for yourself whether the concept makes sense
and is familiar.
If so, then move on. On the other hand, if a whole class of problems is
confusing, make sure to
review that material more thoroughly.
Algebra
For us, "algebra" is just the logical manipulation of variables , numbers, and
the algebraic
operations of addition , multiplication, and exponentiation. We may be trying to
solve an equation
or system of equations , or we may just be rearranging an expression to put it
into a form that is
more useful for our needs. There are a few particular techniques that we will be
using regularly
and we review them here.
1. Linear equations: for each of the following, solve for the unknown
variable (e.g. in the first
one, solve for x).
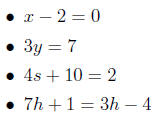
2. Systems of linear equations: for each of the following systems of linear
equations, find all
solutions . (Remember, for linear systems, there may be no solution, exactly one
solution,
or infinitely many solutions.)
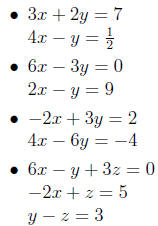
•For the first three systems, graph the equations to verify your solutions.
3. Quadratic expressions: Expand the following (i.e. find an equivalent expression with no parentheses ).
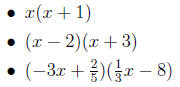
4. The quadratic formula.
•Given the quadratic equation y = ax^2 + bx + c write down
the formula for the roots
of this equation. (It should be familiar and you don't need to derive it.)
•Solve for x in the the following quadratic equations:
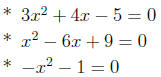
•Use the quadratic formula to find all four roots of the
following fourth degree polynomial: 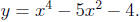
•Use the quadratic formula to find the roots of the equation
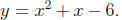 . How does
. How does
this problem relate to the second expression in the above set?
•Graph the equation in the previous step with the roots clearly indicated.
5. Rational expressions are those algebraic expressions
which include a variable in the denominator
somewhere. These types of expressions play a key role in the development of the
derivative. As such, being comfortable with their manipulation will be
important.
•For each of the following expressions, find an equivalent
form involving a single de-
nominator, determine where the expression is equal to zero , and where the
expression
does not exist.
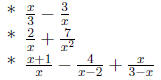
•Consider the following expression:
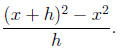
•Note that if you plug in h = 0, the expression formally
reduces to 0/0 , which is undefined.
It turns out we will want to make sense of expressions like these at h = 0 much
better
than simply saying it is undefined. Taking their importance for granted for now,
use
algebra to simplify the expression until you can eliminate the denominator . What
do
you get now when you plug in h = 0?
•The following expression has the same problem at h = 0 as the on above:
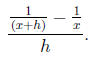
Do a simplification as above (a good first step is to
combine the terms in the numerator ),
and again plug in h = 0 when you are all done. What do you get?
Functions
The primary goal of calculus is to better understand
functions and the way they behave.
Besides working with specific functions, we need to have a solid grasp of what
we can do with
functions in general.
1. Adjusting a function horizontally and vertically: One
of the easiest ways to change a
function is to shift the values that you plug in (resulting in a horizontal
change) or to shift
the values that you get out (resulting in a vertical change). With this in mind,
consider
the following function:
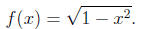
Carefully graph the following in the same coordinate space and indicate which is which:
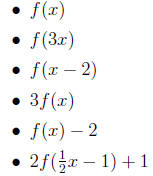
2. Composition of functions: The above adjustments are
special cases of a much more general
technique called composition. The composition of two functions is a new function
determined by taking the output of the first function and using it as input for
the second
function. In other words, given two functions f(x) and g(x), the composition h(x)
= fog(x)
is just f(g(x)). Note that we could compose the functions in the opposite order.
This will
usually result in a different function.
For each of the following, write out (and simplify if
possible) fog(x) and gof(x). Then
graph both compositions.
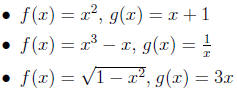 ( Compare with the
second and fourth items in the previous
( Compare with the
second and fourth items in the previous
problem.)
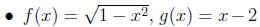 (Compare with the third
and fifth items in the previous
(Compare with the third
and fifth items in the previous
problem.)
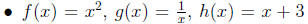 (For this item, note
that you can compose more
(For this item, note
that you can compose more
than two functions. Because the order that the functions are in is important,
there
are actually six different compositions that we can achieve from these three
functions.
You don't have to write them all down or graph them all, but find and graph at
least
three.)
•The last item in the previous problem can be expressed as
a composition of three
functions, one of which is the function f. Find the other two and illustrate the
order
in which these three functions need to be composed in order to get the given
expression.
3. Algebra of Functions: Besides composing functions, we
can do algebra with functions. Let
f(x) = x^2 and g(x) = x+1: For each of the following, write out the resulting
function and
graph it.
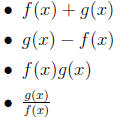
4. Families of Functions: Up until now, we have been
focusing on functions that are algebraic.
There are of course other types of functions with which we will be working. For
each of
the following, determine the domain (where the function is defined) and range
(the values
that you can get out of the function), and carefuly graph the function.
(a) Algebraic
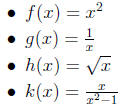
(b) Trigonometric
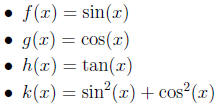
(c) Exponential
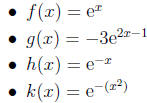
(d) We can, of course, combine these families using
composition and algebra. Choose
three of the above functions (one from each family) and compose them. Determine
the domain and range of your new function and graph it.
| Prev | Next |