Math 2200 Quiz 1 Solutions
Problem 1. (15 points) Show carefully that the compound proposition
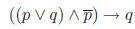
is a tautology.
Proof. We use the laws of propositional logic (also a table of truth values would work).
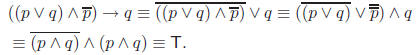
We used the resolution of the implication, one of deMorgan
laws, the double
negation, associativity, and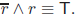
Problem 2. (15 points) Is the following argument
valid? (Carefully
express it in propositional logic, and show the rules of inference used at
each step .)
“You can score well in the GRE only if you have good
analytical skills.
Every student who takes Discrete Math has good analytical skills or good
memory. Maggie doesn’t have good memory. Therefore, if Maggie takes
Discrete Math, then Maggie will score well in the GRE.”
Proof. Define the following propositional functions, where
the domain of the
variable x is “all students”:
• P(x) = x scores well in the GRE;
• Q(x) = x has good analytical skills;
• R(x) = x takes Discrete Math;
• S(x) = x has good memory.
Then the premises of the argument are:
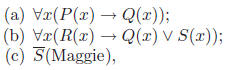
and the conclusion is
(d) R(Maggie) → P(Maggie).
We can use instantiation for (a) and (b) to get
(a’) P(Maggie) → Q(Maggie);
(b’) R(Maggie) → Q(Maggie) ∨ S(Maggie).
From (b’) and (c), we get
(b”) R(Maggie) → Q(Maggie).
But (a) and (b”) do not imply the conclusion (d). The argument is invalid.
Problem 3. (17 points)
(a) Express the following sentence using quantifiers (and logical
propositions ):
“There is a student in this class who has taken some course in every
department in the school of science.”
You should use the variables : s student, c course, d department, and these
should be the only variables. Give the domain of each variable.
(b) Find the logical negation of the quantifier expression that you obtained
in (a).
n (a).
(c) Translate the negation you obtained in (b) into an English sentence.
| Proof. (a) | Variable | Domain |
| s student | this class | |
| c course | all courses | |
| d department | departments in the school of science |
We define the propositional function:
P(s, c, d) = s took course c in department d.
Then the sentence can be written as
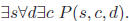
(b) The negation is
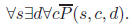
(c) In English: “Every student in this class has not taken any course in
some department in the school of science.”
Problem 4. (18 points)
(a) List the elements of the set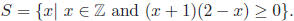
(b) For every integer i ≥ 1, set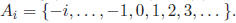 Find
Find
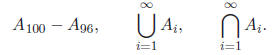
Proof. (a) If (x+1)(2−x) ≥ 0, then −1 ≤ x ≤ 2. Since x is also an integer,
we have S = {−1, 0, 1, 2}.
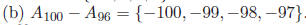
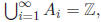 since every nonnegative integer is in
every Ai, and if n is a
since every nonnegative integer is in
every Ai, and if n is a
negative integer , then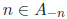
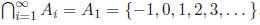 since A1 is
a subset of every Ai.
since A1 is
a subset of every Ai.
Problem 5. (18 points)
(a) Is the function 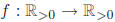 ,
given by f(x) = 3x^2 + 2 one-to-one?
,
given by f(x) = 3x^2 + 2 one-to-one?
What is its image(range)
(b) Consider g :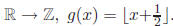 What is
the preimage
What is
the preimage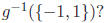
Proof. (a) f is one-to-one (note that the domain is positive numbers ). To see
this, prove the contrapositive: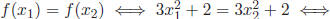
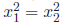 and since x1 > 0, x2 >
0, this is equivalent to x1 = x2
and since x1 > 0, x2 >
0, this is equivalent to x1 = x2
For the image, set y = 3x^2 + 2, then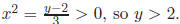 The
image
The
image
is the interval (2,∞). (In particular, f is not onto.)
(b) Recall that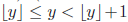 for
every real number y. Then
for
every real number y. Then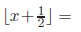
−1, if and only if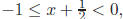 or, equivalently
or, equivalently 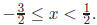
Similarly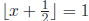 if and only if
if and only if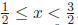
Therefore, the preimage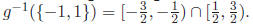
Problem 6. (17 points) Prove the following statements:
(a) For every x > 0, if x is irrational, then
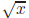 is irrational.
is irrational.
(b) Between any two distinct rational numbers , there exist infinitely many
rational numbers .
Proof. (a) (proof by contrapositive) If
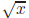 is rational, then x is rational.
is rational, then x is rational.
Write 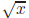 = m/n , for some integers m, n, n ≠ 0.
Then by squaring both sides,
= m/n , for some integers m, n, n ≠ 0.
Then by squaring both sides,
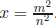 . Since n ≠ 0, then n^2 ≠ 0, moreover, both
m^2, n^2 are integers, since
. Since n ≠ 0, then n^2 ≠ 0, moreover, both
m^2, n^2 are integers, since
m, n are. This proves that x is rational.
(b) (proof by contradiction) Assume that there exist two
rational numbers
a, b, a < b, such that between a and b there are only finitely many rational
numbers.
Then there must be a rational number closest to a among
them, call it r. We have a < r and no rational numbers between a and r.
Consider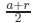 This is a rational number, and
This is a rational number, and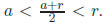 This
gives the
This
gives the
contradiction.
| Prev | Next |