MATH 360 Review of Set Theory
Examples:
1. Let f : R → R be given by f(x) =x2 + 1 and let A =
![]() . Then fA :
A → R
. Then fA :
A → R
has range=(1,∞), whereas f : R → R has a range of [1,∞)
• Note that f is not one-to-one, because if
![]() ∈ R such that
∈ R such that
![]() ,
,
the 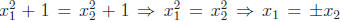 . But we needed
. But we needed
![]() .
.
• Note that fA is one-to-one, because if
![]() ∈ A =
∈ A =
![]() such that
such that
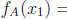
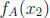 , then
, then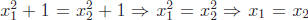 ,
since both must be
,
since both must be
positive reals .
2. Let g : R → R be given by g(x) = sin(π x) and let B = Z. Then
 : B → {0}.
: B → {0}.
The range of  = {0}, whereas the range of g is
[−1, 1]. Note that gB is onto
= {0}, whereas the range of g is
[−1, 1]. Note that gB is onto
the set {0}. Note that  is not one-to-one, and
neither was g. (Why?)
is not one-to-one, and
neither was g. (Why?)
Definition: Let f : X → Y be a one-to-one onto
function. The inverse of f is the
function f -1 : Y → X given by f -1(y) = x iff f(x) = y.
Note: the inverse of the
function is another function.
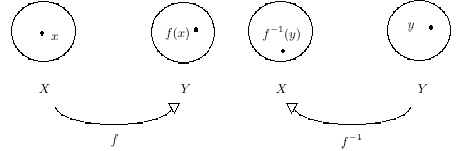
Example: Let f : R →
![]() given by f(x) = ex.
Then f -1(x) = ln(x).
given by f(x) = ex.
Then f -1(x) = ln(x).
Definition: Let f : X → Y be a function and let V 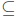 Y . The
inverse image of V
Y . The
inverse image of V
is the set f -1(V ) = {x ∈ X : f(x) ∈ V }.
Very Important Note: The inverse image of a set (just like the image of a
set) is
another set! The inverse of an element (just like the image of element) is an
element.
Here’s the tricky part: the inverse of a function sometimes may not exist. (For
exam-
ple, there is not inverse of the function h : R → R given by h(x) =x2,
since h is not
1-to-1.) But the inverse image of a set ALWAYS EXISTS! (For example, the
inverse
image of [−1, 3] is the set h-1([−1, 3]) = the set of all things in
the domain that map
to the set 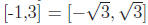 .
.
Examples:
1. Let f : R → R by f(x) = x + 1. Then f-1([2, 3]) = [1, 2].
2. Let g : R → R by g(x) = 4 −x2. Then g-1([2, 3]) =
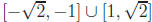 .
.
Theorem: Suppose that f : X → Y is a function S 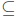 X and T
X and T 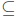 Y . Show that
Y . Show that
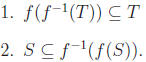
Proof:
1. Let y ∈ f(f -1(T)). Then there exists x ∈ f -1(T) such
that y = f(x) (because
we know that y is in the image of the set f -1(T).) Now for x ∈ f
-1(T) means
that f(x) ∈ T. But remember that f(x) = y! Thus we have y = f(x) ∈ T so
by definition of subsets, f(f -1(T)) 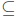 T.
T.
2. Let x ∈ S. Then f(x) ∈ f(S), by definition of the set
f(S). Thus, by definition
of inverse image of a set, x ∈ f -1(f(S)). Thus S 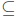 f -1(f(S)).
f -1(f(S)).
Note: In the first proof, my element is y and in the second it is x. This has to
do
with where the elements are actually located: in the domain or in the codomain.
Theorem: Let f : X → Y be a function and let A be a subset of Y . Then f-1(A)
=
X − f-1(Y − A)
Proof: Again, we need to show both 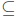 and
and
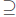 :
:
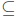 : Let x ∈ f -1(A). Then f(x) ∈ A.
Then f(x)
: Let x ∈ f -1(A). Then f(x) ∈ A.
Then f(x) 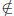 Y −A, so x
Y −A, so x 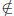 f -1(Y −A). But since
f -1(Y −A). But since
x ∈ f -1(A), by definition of inverse image of a set, x ∈ X. Thus x ∈
X−f -1(Y −A).
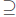 : Let x ∈ X − f -1(Y − A). Then x
∈ X but x
: Let x ∈ X − f -1(Y − A). Then x
∈ X but x 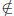 f -1(Y − A). Thus f(x)
f -1(Y − A). Thus f(x) 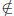 Y − A
Y − A
by definition of inverse images. But if f(x) 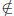 Y − A, and we know that f(x) ∈ Y ,
Y − A, and we know that f(x) ∈ Y ,
because that is the codomain, thus f(x) ∈ A. Thus, by definition of inverse
images,
x ∈ f -1(A).
We have proven both 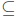 and
and 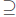 so the equality holds.
so the equality holds.
Theorem: Let f : X → Y be a function and let {Tα : α∈![]() } be an indexed
} be an indexed
collection of subsets of Y . Then
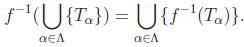
Proof: Suppose x ∈ X.
Then x ∈ f -1(![]() {Tα })
{Tα }) 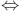
f(x) ∈ ![]() {Tα
}
{Tα
} 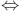
there exists β ∈![]() such
that f(x) ∈ Tβ
such
that f(x) ∈ Tβ 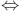
there exists β ∈![]() such that x ∈ f -1(Tβ )
such that x ∈ f -1(Tβ ) 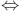
x ∈ ![]() {f -1(Tα
)}.
{f -1(Tα
)}.
Note that the same holds for intersections:  .
.
Example: Let f : R → R be defined by f(x) =x2 + 1 and let =
(0, 1]. For each
α
∈![]() let Vα = [5 −α , 5 +α ]. (For example, V1 = [4, 6], V.5
= [4.5, 5.5].)
let Vα = [5 −α , 5 +α ]. (For example, V1 = [4, 6], V.5
= [4.5, 5.5].)
• We have ![]() {Vα
} = {5}. Thus
{Vα
} = {5}. Thus
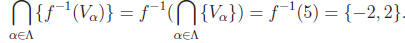
• We have
![]() {Vα
} = [4, 6]. Thus
{Vα
} = [4, 6]. Thus
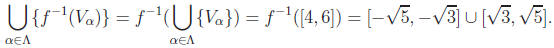
Well, that is all of the set theory that I think we will
need this semester. Cool stuff,
eh?
MATH 360 - Set Theory Homework Assignment
1. Let X = R, A = (−2, 4],B = [0, 3),C = (−∞, 0) and D = [0, 4]. Find each of
the following sets. In parts (j) and (k) sketch the region.
(a) A − B
(b) A ∪ C
(c) B ∩ C
(d) (A ∪ B) − D
(e) X − A
(f) X − C
(g) (A ∩ B) ∩ D
(h) (A ∪ B) ∩ D
(i) B − A
(j) X × A
(k) B × C
2. Let A and B be subsets of X. Prove the other one of DeMorgan' s Laws :
X − (A ∩ B) = (X − A) ∪ (X − B)
3. Prove the following: A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
4. Let A and B be subsets of X. Show that A ∩ B = 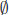 iff A
iff A 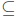 X − B.
X − B.
5. Find the sets indicated.
(a) = ![]() and for each α ∈
and for each α ∈![]() let Aα = [−π ,α ). Find
let Aα = [−π ,α ). Find
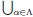 {Aα
}
{Aα
}
and ![]() {Aα
}.
{Aα
}.
(b) = 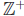 and for each α ∈
and for each α ∈![]() let Bα = (
α, α + 3). Find
let Bα = (
α, α + 3). Find
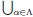 {Bα
}
{Bα
}
and ![]() {Bα
}.
{Bα
}.
6. Let {Aα
:α ∈![]() } be an indexed collection of subsets of X. Prove the other one
} be an indexed collection of subsets of X. Prove the other one
of DeMorgan’s Laws for indexed collections of sets:
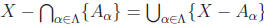
7. Suppose {Aα
:α ∈![]() } is an indexed collection of subsets of X and S
} is an indexed collection of subsets of X and S 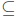 X.
X.
Then
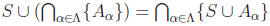
(Note: the following is also true, but is not a homework problem:
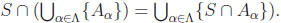
8. Let f : X → Y be a function and let {Aα
:α ∈![]() } be an
indexed collection of
} be an
indexed collection of
subsets of X. Then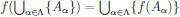 .
.
9. Let f : X → Y be a function and let U 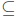 X
and V
X
and V 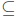 X. Prove that
X. Prove that
f(U) − f(V ) 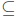 f(U − V ).
f(U − V ).
10. Let f : X → Y, g : Y → Z be functions.
(a) Prove that if both f and g are onto, then g o f : X → Z is onto.
(b) Prove that if g o f is one-to-one, then f is one-to-one.
11. Find an example ( different than the one given in class) of a function f : X
→ Y
and A 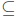 X such that
X such that
(a) f|A : A → Y is one-to-one, but f is not one-to-one.
(b) f : X → Y is onto and f|A : A → Y is not onto.
12. Let f : X → Y be a function and let {Tα
: α ∈![]() } be an indexed collection of
} be an indexed collection of
subsets of Y . Show that  .
.
| Prev | Next |