Math 75 Notes
Math 75 Notes
1 Euclid's algorithm and Z/(p)
We start at a place that might seem a bit far a field:
Euclid's algorithm from elementary number
theory for finding the greatest common divisor of two integers. Take the example
of the integers
91 and 143. We start Euclid's algorithm by taking the smaller of the numbers,
91, into the
larger; this goes in once and leaves a remainder of 52. We then take the
remainder, 52, into the
last divisor, 91. This goes in once, and we find a new remainder of 39. We keep
this process
up until one of these divisions works out without any remainder. According to
Euclid, the last
nonzero remainder (13 in this case) is the gcd:
143 = 91 · 1 + 52
91 = 52 · 1 + 39
52 = 39 · 1 + 13
39 = 13 · 3 + 0:
For another example we could take the numbers 7 and 17:
17 = 7 · 2 + 3
7 = 3 · 2 + 1
3 = 1 · 3 + 0;
so that in this case Euclid's algorithm tells us that 7
and 17 are relatively prime: their only
common positive divisor is the number 1.
It is tempting to suppose that Euclid's algorithm was
wasted on our last example. Indeed,
17 is a number which is immediately recognizable as a prime, so that it is
obvious it has no
factors in common with the smaller integer 7. But our e ort is not in vain!
Indeed, for our
purposes it is not the final answer of Euclid's algorithm (which we could have
predicted was 1
immediately) that is of interest, but the intermediate steps to reach that
outcome which are of
most interest.
These computations allow us to express 1 as a linear
combination of 17 and 7. We start by
writing
3 = 17 - 7 · 2,
which comes from the first of our Euclidean steps above.
Thus we have 3 as a linear combination
of 7 and 17. Next we write
1 = 7 - 3 · 2;
which is the result of transposing the second Euclidean
step above. This gives 1 as a combination
of 7 and 3. But we determined that 3 = 17 · 1 + 7(-2),
and so
1 = 7 · 1 - (17 · 1 + 7(-2))2 = 7 · 5 + 17(-2):
And now if we look at this equation in the system Z =(17), where 17 = 0, we find that
1 = 7 · 5.
So our computation with Euclid's algorithm has earned its
keep: it allowed us to construct an
inverse of 7 modulo 17.
More generally, Euclid's algorithm gives one a
constructive proof of the following important
result:
Theorem 1. Let a; b be integers, not both zero, and
let d be the greatest common divisor of a
and b. Then there are integers x and y with
ax + by = d:
In particular, if a and b are relatively prime, then one can solve the equation
ax + by = 1:
This allows us to settle one of our outstanding debts. We
can now prove the following result,
mentioned in the introductory lecture:
Theorem 2. Let p be a prime. Then Z/(p) is a eld.
The proof is now easy. We already know everything we need
to know about F = Z/(p),
except for the existence of multiplicative inverses for everything in F \ {0}.
But Z/(p) =
{0, 1,…, p - 1}, and so F \ {0} = {1, 2,…, p - 1}. Each of a = 1, 2, 3,…, p - 1 are relatively
prime to p, so that we can solve
ax + py = 1:
Reading this equation in Z/(p), we see that ax = 1, so that a has an inverse modulo p. Done!
It is worth emphasizing that the way we have proved this
result not only shows the existence
of inverses but gives an algorithm for computing them.
Example 1. Let p = 101 and a = 11. Find a-1 in Z/(p).
Solution . We begin by performing Euclid's algorithm on the integers 11 and 101:
101 = 11 · 9 + 2
11 = 2 · 5 + 1
2 = 1 · 2 + 0:
Now we solve for 1 as a linear combination of 11 and 101:
2 = 101 + 11 · (-9)
1 = 11 + 2 · (-5)
= 11 + (101 + 11 · (-9)) · (-5)
= 11 · 46 + 101 · (-5):
Reading this last equation in Z/(101), we see 1 = 11 46. So 46 is the inverse of 11.
2 Constructing new fields from old
The insight that Z/(p) is a field is from the viewpoint of generalization a rather
fundamental
one. Cast in broad terms , we started with a system Z (not itself a field) and
created a field
by supplementing the arithmetic of Z with a new equation 'p = 0' for a prime p.
In order to
understand all finite fields, we will use a similar construction, but with systems
other than Z
as our starting points. We now introduce these systems.
Let F be a field. We de fine the univariate polynomials over F in the indeterminate
x as
the set of expressions of the form
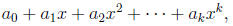
where all the ai belong to F. The degree of a polynomial is the highest power of
x that appears
with a nonzero coefficient ; for example, over R, the polynomial 3x2 + 1 has degree
2 and the
constant polynomial 1 = 1x0 has degree 0. The polynomial 0 (corresponding to
choosing all
the ai above to equal zero) has no powers of x which appear with a nonzero coefficient; we leave
its degree undefined.
When the field F is the field of real or complex numbers , these definitions are
familiar, but
they work just as well over any field (e.g., Z/(p) for a prime p). Moreover, the
usual operations
of addition and multiplication for polynomials make sense in this general
context. For example,
let F = Z/(5), and de ne A,B ∈ F[x] by
A = 3x3 + x + 1, B = 4x + 2:
Then
A + B = 3x3 + 5x + 3 = 3x3 + 3
(recalling that 5 = 0 in Z/(5)) while
AB = 12x4 + 6x3 + 4x2 + 2x + 4x + 2
= 12x4 + 6x3 + 4x2 + 6x + 2
= 2x4 + x3 + 4x2 + x + 2:
With these definitions of +, . , the system F[x] becomes what is called a commutative ring:
• it is an abelian group under addition (with additive identity the polynomial 0),
• `. ' distributes over `+': for all A,B,C ∈ F[x], we have A(B + C) = AB + AC,
• there is a multiplicative identity (the constant polynomial 1),
•
multiplication is commutative (AB = BA for all A,B ∈ F[x]) and associative
(i.e.,
A(BC) = (AB)C for all A,B,C ∈ F[x]).
These properties look very close to the properties singled out in our definition
of a field. Nev-
ertheless, F[x] is not a field. In a field every nonzero element has an inverse, but
it turns out
that there are relatively few elements of F[x] which are invertible. We call
invertible elements
units.
| Prev | Next |