Matrix Algebra

Matrices A matrix is a rectangular array of elements arranged in rows and columns. A matrix
is usually denoted by a boldface capital letter. For example:

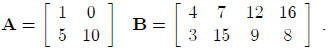
The dimension of the matrix A is 2×2 (2 rows by 2 columns) and the dimension of matrix B is
2 × 4 (2 rows by 4 columns). Note that in giving the dimension of matrix, we always specify the
number of rows first and then the number of columns.

As in ordinary algebra , we may use symbols to identify the elements of a matrix:

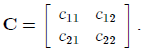
Note that the first subscript identifies the row number of the second the column number. We shall
use the general notation a_ij for the element in the ith row and the jth column. In our example
above, i = 1, 2 and j = 1, 2.

A matrix is said to be square if the number of rows equals the number of columns. Two examples
are:

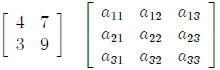
A matrix containing only one column is called a column vector or simply a vector. Two examples
are:

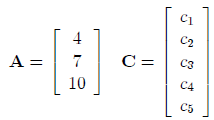
The vector A is a 3 × 1 matrix and the vector C is a 5 × 1 matrix.
A matrix containing only one row is called a row vector. Two examples are:

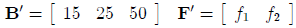
We use the prime symbol for row vectors for reasons to be seen shortly. Note that the row vector
B' is a 1 × 3 matrix and the row vector F' is a 1 × 2matrix.

The transpose of a matrix A is another matrix, denoted by A', that is obtained by interchanging
corresponding columns and rows of the matrix A. For example, if:

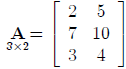
then the transpose A' is:

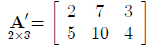
Note that the first column of A is the first row of A' and, similarly, the second column of A is the
second row of A'. Note that the dimension of A, indicated under the symbol A, becomes reversed
for the dimension of A'. Note that the transpose of a column vector is a row vector, and vice versa.
This is the reason why we used the symbol B' earlier to identify a row vector, since it may be
thought of as the transpose of a column vector B.

Two matrices A and B are said to be equal if they have the same dimension and if all corresponding
elements are equal. Conversely, if two matrices are equal, their corresponding elements
are equal.

Matrix Addition and Subtraction Adding or subtracting two matrices requires that they have
the same dimension. The sum, or difference , of two matrices is another matrix whose elements each
consist of the sum, or difference, of the corresponding elements of the two matrices. Suppose:

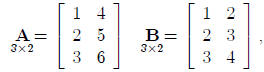
then:

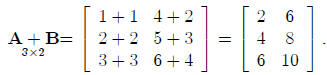
Similarly:

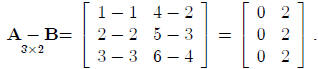
Note also that A+B = B+A, as in ordinary algebra.

Matrix Multiplication A scalar is an ordinary number or symbol representing a number. In
multiplication of a matrix by a scalar, every element of the matrix is multiplied by the scalar. For
example, suppose the matrix A is given by:

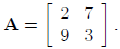
Then 4A, where 4 is the scalar, is:

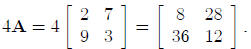
Multiplication of a matrix by a matrix may appear somewhat complicated at first, but a little
practice will make it a routine operation . Consider the two matrices:

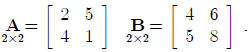
The product AB will be a 2 × 2 matrix whose elements are obtained by finding the cross products
of rows of A with columns of B and summing the cross products. For instance, to find the element
in the first row and the first column of the product AB, we work with the first row of A and the
first column of B, as follows:

2(4) + 5(5) = 33.

Continuing this process, we find the product AB to be

Let us consider another example:

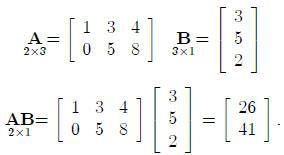
When obtaining the product AB, we say that A is postmultiplied by B or B is premultiplied by
A . The reason for this precise terminology is that multiplication rules for ordinary algebra do not
apply to matrix algebra. In ordinary algebra, xy = yx. In matrix algebra, AB ≠ BA usually. In
fact, even thought the product AB may be defined, the product BA may not be defined at all. In
general, the product AB is only defined when the number of columns in A equals the number of
rows in B so that there will be corresponding terms in the cross products.

Special Types of Matrices If A = A', A is said to be symmetric. Thus, A below is symmetric:

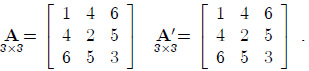
A symmetric matrix necessarily is square.
A diagonal matrix is a square matrix whose off-diagonal elements are all zeros, such as:

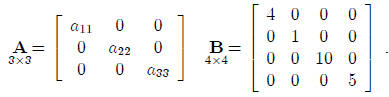
The identity matrix or unit matrix is denoted by I. It is a diagonal matrix whose elements on
the main diagonal are all ones. Premultiplying or postmultiplying any r ×r matrix A by the r ×r
identity matrix I leaves A unchanged. For example:

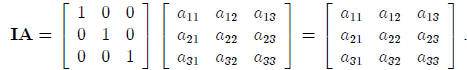
Similarly, we have:

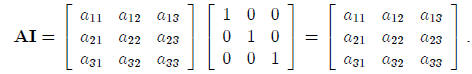
Note that the identity matrix I therefore corresponds to the number 1 in ordinary algebra, since we
have ether 1x = x1 = x. In general, we have for any r × r matrix A:

AI = IA = A.

A column vector with all elements 1 will be denoted by 1:

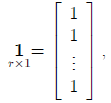
and a square matrix with all elements 1 will be denoted by J:

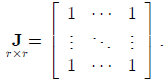
Note that for any n × 1 vector 1, we obtain:

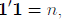
and:

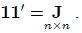
A zero vector is a vector containing only zeros. The zero column vector will be denoted by 0:

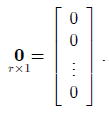
Inverse of a Matrix In ordinary algebra, the inverse of a number is its reciprocal. Thus, the
inverse of 6 is 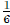. A number multiplied by its inverse always equals 1. In matrix algebra, the inverse
of a matrix A is another matrix, denoted by A^-1, such that:

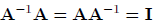
where I is the identity matrix. Thus, again, the identity matrix I plays the same role as the number
1 in ordinary algebra. An inverse of a matrix is defined only for square matrices. Even so, some
square matrices do not have an inverse. If a square matrix does have an inverse, the inverse is
unique. For example, the inverse of the matrix:

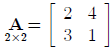
is:

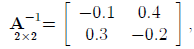
since:

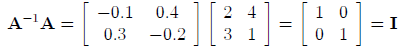
and:

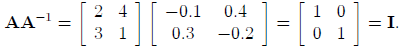
Note that the inverse of a diagonal matrix is a diagonal matrix consisting simply of the reciprocals
of the elements of the diagonal.

Finding the inverse of a matrix can often require a large amount of computing. We shall take
the approach that the inverse of a 2 × 2 matrix can be calculated by hand . For any larger matrix,
one ordinarily uses a computer or programmable calculator to find the inverse, unless the matrix is
of a special form such as a diagonal matrix. If:

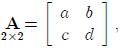
then

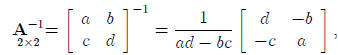
where D = ad- bc is called the determinant of the matrix A. If the determinant of A would equal
zero, then A is said to be singular and no inverse exists.

Solving Simultaneous Equations Using Matrices In ordinary algebra, we solve an equation
of the type:

5y = 20

by multiplying both sides of the equation by the inverse of 5, namely:

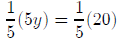
and we obtain the solution:

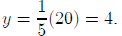
In matrix algebra, if we have an equation:

AY = C,

we correspondingly premultiply both sides by A^-1, assuming A has an inverse:

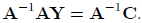
Since 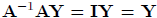, we obtain the solution:

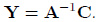
To illustrate this use, suppose that we have two simultaneous equations:

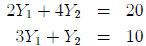
which can be written as follows in matrix notation:

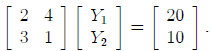
The solution of these equations then is:

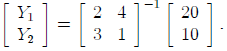
Earlier we found the required inverse, so we obtain:

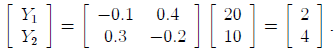
Hence, Y₁ = 2 and Y₂ = 4 satisfy these two equations.