More on Exponents and Like Terms
A subtle but important addition to the order of operations is illustrated by the following. If you have

you should view the −- sign as being mulitiplied, like
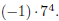 The exponent , therefore, should be evaluated
The exponent , therefore, should be evaluated
first
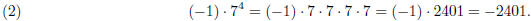
On the other hand, in

the order of operations say to apply the negative sign first. Here we get
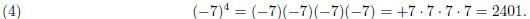
Since pairs of negatives multiplied together are positive,
even numbers of −’s are positive and odd numbers
of −’s are negative. So we get a negative number out of

You should be using your calculator for these , but you
should know how the sign is going to come out
beforehand.
Quiz 08, Part I
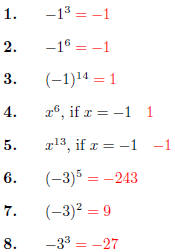
Combining like terms
Consider an expression like

As we did before, we can factor out the common factor
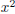 (or both factors of x). This would give us
(or both factors of x). This would give us
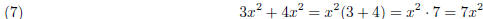
Another way of thinking about this, we’re adding a bunch
of x2’s, three of them and then four more, for a
total of seven.
In general, as long as the variable parts are the same, then we can add the coefficients. For example,

This is called combining like terms . When we want to get
to an expanded form (as opposed to factoring),
we’ll combine like terms, and leave the unlike terms apart. For example,

We can factor this, of course, but keep in mind where you
want to end up. If you’re multiplying everything
out, this is the form you want.
Here are a few more examples.
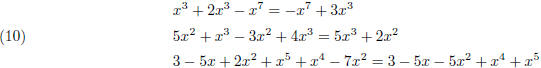
It is customary to arrange the terms from lowest power to highest or the other way, from highest to lowest.
Quiz 08, Part II
Combine like terms, and put in simplified expanded form. Giving terms in
reverse order is fine.
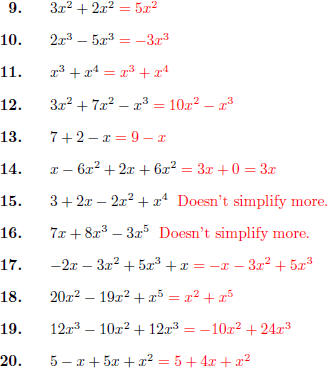
Homework 08
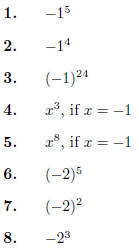
Combine like terms, and put in simplified expanded form .
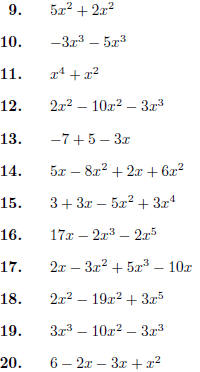
| Prev | Next |