Proofs

Example 2. Prove the following results:

(a) If c is a non- zero rational number, then c π is irrational.
(b) If m³ is even, then m is even.
(c) For all real numbers x and y , if x + y > 0, then x > 0 or y > 0.
(d) Let n be an integer. If n² is divisible by 3, then n is divisible by 3.
(e) Let x be a real number . If 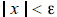for all 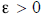, then x = 0 .

(a) Proof. (By contradiction) Let c be a non-zero rational number , and suppose that c π
is rational. Then c π = m / n , where m , n are integers and n ≠ 0. Moreover, c = j / k ,
where j , k are integers and k ≠ 0, but also j ≠ 0 because c is non-zero. We then have

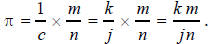
The products of integers k m and jn are still integers, and jn cannot be 0 because
neither n nor j is 0. Thus, π is in the form of a rational number, which is a
contradiction because π is irrational. Ergo, c π must be irrational. QED
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

(b) Claim: If m³ is even, then m is even. We shall prove the contrapositive instead; we
shall assume that m is not even and show that m³ is not even. That is, we shall assume
that m is odd and show that m³ is odd.

Proof. Assume that m is odd. Then m = 2 k +1 for some integer k . Then,

m³
= (2 k + 1)³
= 8k³ +12k² + 6k + 1
= 2(4k³ + 6k ² + 3k) + 1
= 2l + 1,

where l is the integer 4k³ + 6k² + 3k . Thus, m³ is odd because it is written in the form
of an odd integer. By contrapositive, if m³ is even, then m is even. QED
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

(c) Proof. Let x and y be real numbers. Assume that x ≤ 0 and y ≤ 0. Then by adding ,
we have x + y ≤ 0 + 0 = 0. That is, x + y ≤ 0. Hence, x ≤ 0 and y ≤ 0 implies that
x + y ≤ 0. By contrapositive, if x + y > 0, then x > 0 or y > 0. QED

(d) Claim: For an integer n , if n² is divisible by 3, then n is divisible by 3.

Proof. Assume n is not divisible by 3. We then can apply the Fundamental Theorem of
Arithmetic to write n uniquely as a product of powers of primes as follows:

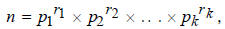
where r_i are natural numbers and the p_i are distinct primes. Because n is not divisible
by 3, then p_i ≠ 3 for 1 ≤ i ≤ k . By squaring we obtain

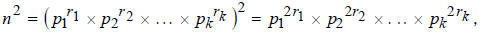
which is a prime factorization of n ². By uniqueness of prime factorization, the above p_i
for 1 ≤ i ≤ k are the only prime factors of n ². Because none of the p_i equals 3, then n² is
not divisible by 3. By contrapositive, if n² is divisible by 3, then n must also be divisible
by 3. QED
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Note: The preceding result can be generalized as follows:
Let p be prime and suppose k ≥ 2 . If n^k is divisible by p , then n is divisible by p .
(In the proof of (d), simply replace 3 with p and replace the exponent 2 with k .)
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

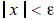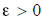(e) Claim: If all , then x = 0 .

Proof. Suppose 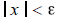all 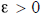We must show that x = 0 . So suppose that x ≠ 0 .
Then x < 0 or x > 0. In either case, we have 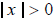. Now let 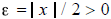. For this
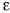, we then have 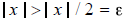, which contradicts the assumption. Thus we must
have that x = 0 . QED

Note: We also could have argued by contrapositive: Assume x ≠ 0 . Then we showed
that there exists an 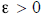for which 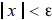fails. So if x ≠ 0 , then it is not true that
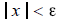for all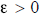. By contrapositve, if it is true that 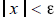for all 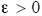, then x = 0 .

Double Implication

A double implication is of the form p ↔ q, which is read “ p if and only if q ”. This
statement means p → q and q → p and both implications must be proven.

Example 3. Let n be an integer. Then n is even if and only if n² is even.

Proof. Suppose first that n is even. Then n = 2k , for some integer k . So then

n² = (2 k )² = 4k² = 2(2k² ).

Because 2k² is also an integer, we see that n² must be even.

Next we must prove that if n² is even, then n is even. But we shall prove the
contrapositive instead. So assume that n is not even, i.e., that n is odd. Then n = 2k +1
for some integer k . We then have

n² = (2k +1)² = 4k ² + 4k + 1 = 2(2k² + 2k) +1 = 2 j +1,

where j = 2k² + 2k is an integer. Hence, n² is odd; that is, n² is not even. We have
proven that if n is not even, then n² is not even. By contrapositive, if n² is even, then n
is even. From both directions, we now have that n is even if and only if n² is even.
QED

Note: The second direction also follows from the generalization of Part (d) using the
prime p = 2 . In other words, if 2 divides n² then 2 divides n .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Theorem. 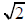is irrational.

Proof. Assume 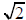is rational. Then we can write 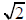= m / n , where m and n are
integers with n ≠ 0. Furthermore, we can assume that the fraction is reduced so that m
and n have no common divisors . Then by squaring the fraction , we have

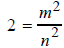or 2n² = m² .

Thus, m² is even because it is divisible by 2. It follows that the integer m must be
even (by Example 3). So we may write m = 2k for some integer k . Then

2n² = m² = (2 k)² = 4k ² = 2(2 k² ), which gives n² = 2k ².

Thus, n² is even because it is divisible by 2. It follows that the integer n also must
be even. So both m and n are even and therefore both are divisible by 2. But this fact
contradicts the assumption that we have chosen m and n to have no common divisors .
This contradiction leads us to conclude that 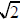cannot be written as a fraction . Thus,
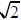is irrational.  QED

Corollary. For any prime p , 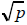is irrational.

Exercises

Prove the following results in a formal, elegantly written, mathematical style :

(a) For all integers m and n , if m is even and n is odd, then m + n is odd.

(b) Let a be an integer. If a divides b , then b is an integer and a divides b².

(c) If x and y are rational numbers, then x + y is a rational number.

(d) Let m and n be integers. If m n is even, then m is even or n is even.

(e) Let m and n be integers. If m + n is odd, then m is odd or n is odd but not both.

(f) Let x and y be real numbers. Then x = y if and only if 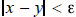for every .

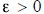(g) For any prime p , 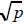is irrational.