Quadratic Inequalities
An inequality expresses the relation between two
expressions where one is greater than the other.
Unlike equations , inequalities typically have an infinite number of solutions
(and an infinite number of
non-solutions).
We solved inequalities in elementary algebra using the
techniques for solving equations:
EX: Solve: 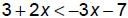
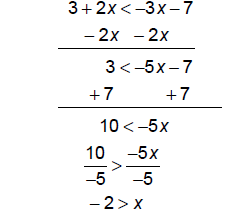
Note that when dividing or multiplying by a negative we
must reverse the inequality symbol since
"largeness" reverses when we move from the negative to the positive side of the
number line. For
example, 5 > 3 but -5 < -3.
We can show the infinite number of solutions on a number line.
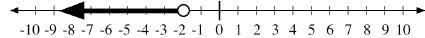
Note the open circle at -2 to indicate that -2 is NOT part
of the solution.
We can write the solution as follows:
-2 > x
or x < -2
or {x | x < -2}
or (-∞,-2)
We can check the solution by replacing x with a value that
is in the solution set and seeing if it
satisfies the inequality. We can also choose a "non-solution" and see if that
does NOT work.
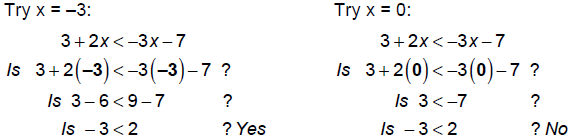
We can also think of
3 + 2x < -3x - 7 in terms of functions .
For example:
Let f (x) = 3 + 2x and g (x) = -3x - 7
Solve f (x) < g (x) .
That is, find the values of x where f < g.
f and g are two lines that we can easily graph:
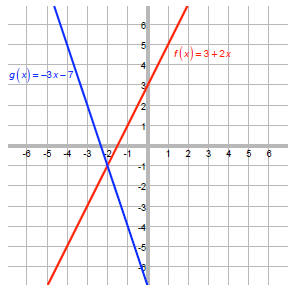
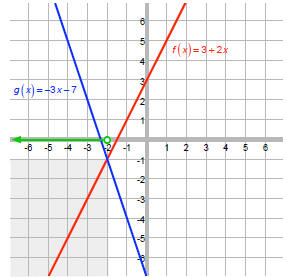
We want the values of x where the blue g is above (greater than) the red f.
We can see that g is above f when x is less than –2.
That is, the solution to f (x) < g (x) is {x | x < -2} .
EX: Consider the function f (x) = x2 - 6x + 5 . Solve the
inequality f(x) < 0
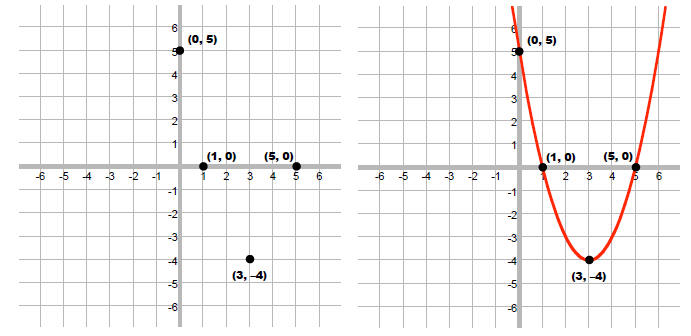
We can graph the function and locate the region where the graph is below the
x-axis.
vertex:
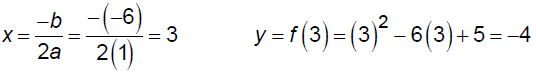
x-int:
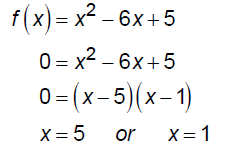
y-int:
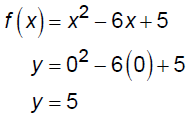
Since we want
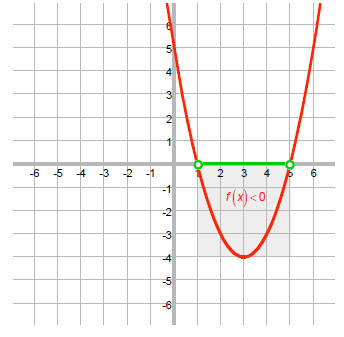
f (x) < 0 , we are looking for the values of x where f is below the x-axis.
Thus, the solution is {x |1< x < 5}.
Let's check 3 values:
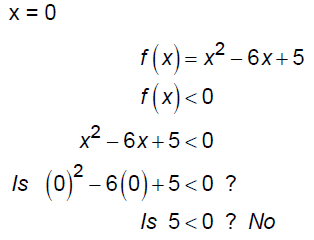
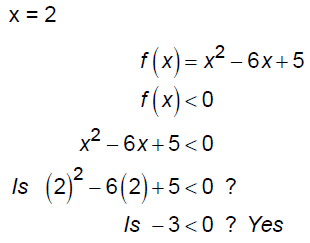
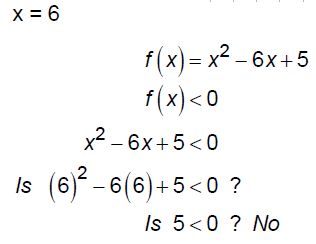
EX: Solve the inequality: -x2 < 4x -12
We can solve this in several different ways .
Method A : Move all terms to one side of the inequality:
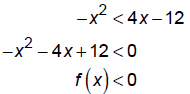
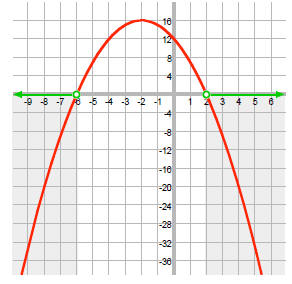
Now, graph the functionf (x) = -x2 - 4x +12
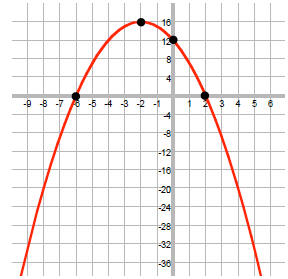
The vertex is (-2, 16), the x-intercepts are (-6, 0) and
(2, 0), and the y-intercept is (0, 12).
On the graph, note where the function is below the x-axis:
So, the solution is {x | x < !6 or x > 2}
Note that if we rearrange the inequality into an
equivalent
inequality we will get a different graph but the same solution.
For example:
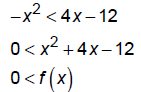
This is an upward opening parabola with vertex (-2, -16),
x-intercepts (-6, 0) and (2, 0), and y-intercept (0, -12).
Here, we want to locate the values of x where the function is
positive rather than negative. The solution is the same as
before, {x | x < -6 or x > 2} .
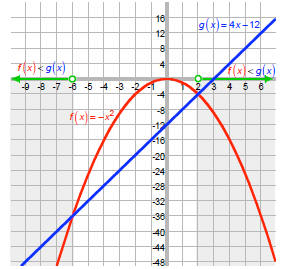
Method B: We can also solve -x2 < 4x - 12 by defining two
functions and then finding the values of
x where one is greater than the other.
Let f (x) = -x2 and g (x) = 4x - 12 .
We have a standard downward opening parabola and a line
of slope 4 and y -intercept -12.
How, we want to know for which values of x we have
f (x) < g (x) . On the graph, these are the values of x where
the red f(x) is below the blue g(x).
We get the same solution as before.
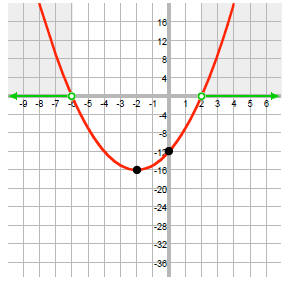
Method C: We can also solve -x2 < 4x - 12 algebraically, without graphing.
Step 1: Rearrange the inequality: 0 < x2 + 4x - 12 Now, we want to know for
which values of x is
0 < f (x). In other words, when is this function positive?
Step 2: Factor the expression:
f (x) = x2 + 4x - 12
= (x - 2)(x + 6)
We want to know when this product is positive ; that is, when
0 < f (x). That will be the case when
the signs of the two factors are the same (both negative or both positive).
Step 3: We know that the only way a factor can switch sign is when it passes
through 0. So, separate
the number line into intervals using values where the factors are 0:
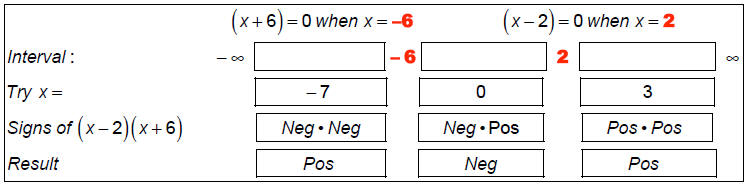
Step 4: Determine the region where the function obeys the inequality, 0 < f (x).
We can see that the function is positive in the intervals x <
-6 and x > 3.
We will use this technique when solving inequalities involving rational
polynomials in section 4.4
p157 #36
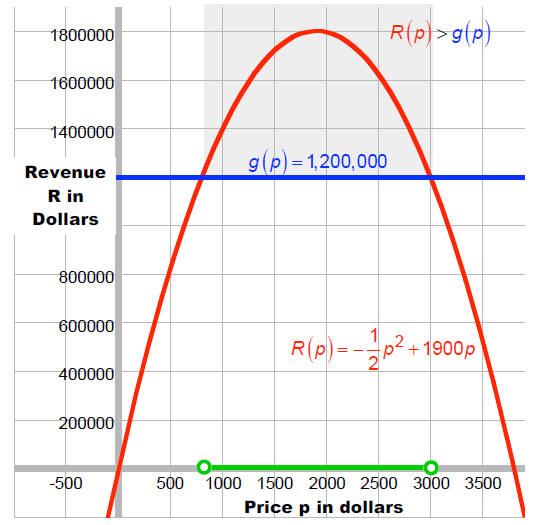
John Deere found that the revenue of tractors is given by R(p) = -(1/2)p2 +1900p
where p is the unit
price in dollars. For what range of prices will revenue exceed 1,200,000?
Let R(p) = -(1/2)p2 +1900p and g (p) = 1,200,000. We want
to know for what values of p is
R(p) > g (p) .
From the graph we can estimate the solution as:
{p | 800 < p < 3000}.
EX: Solve 25x2+16 < 40x
Let's solve this algebraically:
Step 1: Rearrange the inequality: 25x2- 40x +16 < 0 Now, we want to know for
which values of x is
f (x) < 0 . In other words, when is this function negative?
Step 2: Factor the function:
25x2- 40x +16 < 0
(5x - 4)(5x - 4) < 0
We want to know when this product is negative. That will be the case when the
signs of the two
factors are different.
Step 3: Separate the number line into intervals using values where the factors
are 0. The zeros of the
factors are
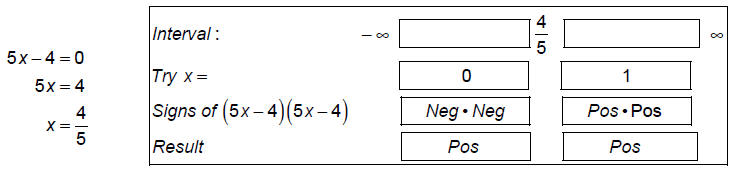
Step 4: Determine the region where the function obeys the
inequality,
f (x) < 0 . The function is never
negative so the answer is no solution.
Note that we could have seen this by writing (5x - 4)(5x - 4) < 0 as (5x - 4)2<
0 .
The square of a real number cannot be negative so right here we can see that
there is no solution.
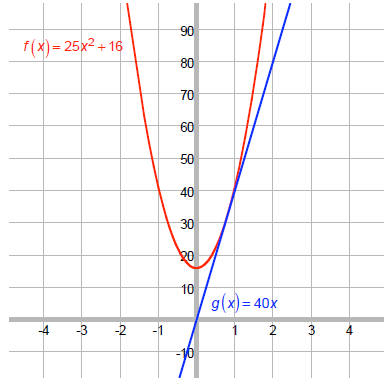
Let's check this using graphs:
Let f (x) = 25x2+16 and g (x) = 40x .
We want the values of x where f (x) < g (x) :
We see that g is never above f, although it
appears that g and f touch at about x = 4/5.
EX: Solve x(x +1) > 20
Let's solve this algebraically:
Step 1: Rearrange the inequality: x2 + x - 20 > 0 Now, we want to know for
which values of x is
f (x) > 0 . In other words, when is this function negative?
Step 2: Factor the function:
x2 + x - 20 > 0
(x - 4)(x + 5) > 0
We want to know when this product is negative. That will be the case when the
signs of the two
factors are different.
Step 3: Separate the number line into intervals using values where the factors
are 0 as cutoffs. The
zeros of the factors are at x = 4 and x = -5.
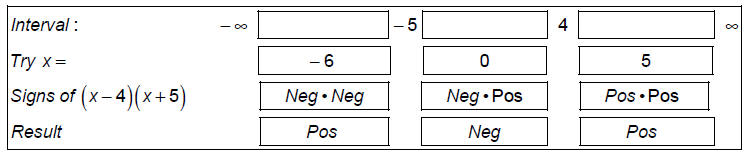
Step 4: Determine the region where the function obeys the inequality,f (x) > 0 .
This is {x | -5 < x or x > 4}
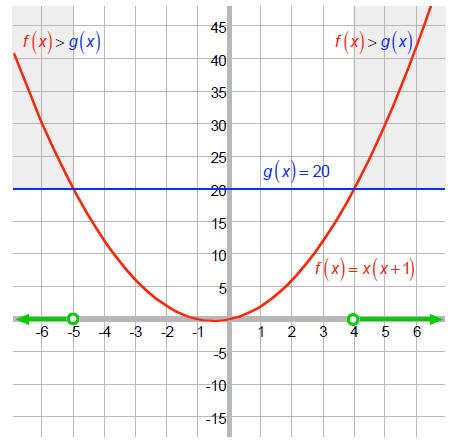
Let's check this using graphs:
Let f (x) = x(x +1) and g (x) = 20 .
We want the values of x where
f (x) > g (x) :
We see that f is above g when
x < -5 or when x > 4.
| Prev | Next |