Review of Exponential and Logarithmic Expressions and Functions
Review of Exponential and Logarithmic Expressions and Functions
Exponential and Logarithmic Expressions :
An exponential expression is an expression involving an
exponent. Typically when we refer to
exponential expressions, we do assume the base is a constant and the exponent is
a variable, such as
ax . a must be a non-negative number and preferably greater than 1. (Why is
this, you might ask?
Because negative numbers don ’t play well with non-integer exponents since
fractional exponents
represent roots and you can’t take square roots (and other even-indiced roots)
of negative numbers.
Zero is not a good base because when raised to a negative power you put a zero
in the denominator of a
fraction. Finally, 1 is discouraged since 1 to any power is still 1.)
A special base for an exponential expression in the number
e (recall that e ≈ 2.71828 and is an irrational
number similar to pi). The expression ex is called the natural exponential and
e is the natural base. ex
is very useful and important in calculus.
A logarithmic expression represents an exponent. The value
of a logarithm is equal to the exponent
needed to raise the base to equal the input. (Read the last two statements over
and over – they
represent the foundation of logarithms.) Logarithmic expressions are written in
the form loga x where a
would be the base of the logarithm and x is the input. (This logarithm would be
read “the logarithm base
a of x”.)
Examples:
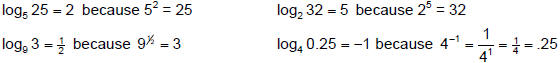
Two special logarithms:
Common logarithm – logarithm base 10
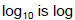
Natural logarithm – logarithm base e
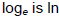
Special properties of all logarithms :
loga 1 = 0 because anything to the 0 power
is 1
loga a = 1 because anything to the first power is itself
loga ax = x because the base must be raised to the x power
Laws applied to logarithms include:
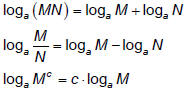
Important by-product – the change of base formula :

Just as addition and subtraction, multiplication and division, and powers and
roots are all examples of
inverse operations – where one action undoes the effect of the other –
exponentials and logarithms with
the same base are inverse operations of each other.
Thus
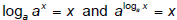 because the composition (one operation inside another
operation) of
because the composition (one operation inside another
operation) of
inverse expressions should return the input of the inside operation.
Exponential Functions:
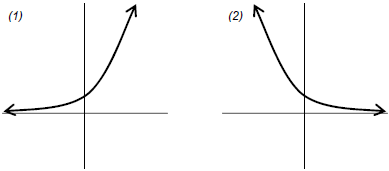
f (x) = ax , a > 0, a ≠ 1 a is the base and is a constant
| Domain: (−∞,∞) | Range: (0,∞) | |
| y- intercept : (0,1) | no x-intercept | horizontal asymptote: y = 0 |
If a > 1, then the function is always increasing with a graph like (1) below.
If 0 < a < 1, then the function is always decreasing with a graph like (2)
below.
Transformations can be applied to shift, reflect, or stretch/shrink the
function.
Logarithmic Functions: f (x) = loga x, a > 0, a ≠ 1 a is the base
| Domain: (0,∞) | Range: (−∞,∞) | |
| x-intercept: (1,0) | no y-intercept | vertical asymptote: x = 0 |
If a > 1, then the function is always increasing with a graph like (3) below.
If 0 < a < 1, then the function is always decreasing with a graph like (4)
below.
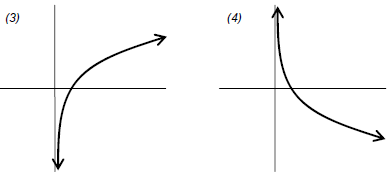
Transformations can be applied to shift, reflect, or stretch/shrink the
function.
Generalized Rules for solving Exponential & Logarithmic Equations
Unless you have a special form that can be factored first , most exponential
equations can be solved as
follows:
If there is just one exponential expression in the equation:
a: take all necessary steps to isolate the expression on one side
b: take the common or natural logarithm of both sides
- traditionally the common log is used, but I tend to take the natural log in
order
to avoid the confusion that the common log (which looks like any other
logarithm except without a stated base) sometimes present… you should
always use common log with base 10 exponentials and natural log with base
e exponentials
c: use the laws of logarithms to rewrite the expression without exponents
d: solve for the variable
If there are two exponential expressions in the equation:
a: follow steps (b) and (c) above
b: since they will most likely be more than one variable term involved , follow
steps
involving grouping and factoring to isolate the variable on one side
c: then solve for the variable
Exception to the previous case – if the bases of the two exponential expressions
are equal, then
to solve you simply set the exponents equal to each other. If the two
exponential expressions are
related by some power or root, use exponential laws to rewrite them so that you
have equivalent
bases, then set the exponents equal to each other and solve.
Some exponential expressions can be factored similar to
quadratics. Remember
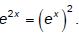
Solving logarithmic equations can be divided into two broad categories – those
that can be written where
a logarithm is equal to a number and those that can be written where logarithms
of the same base are
equal to each other. Use the laws of logarithms to rewrite multiple logarithmic
expressions as a single
log, then use the appropriate case:
If a logarithm is equal to a number, rewrite as an exponential and solve.
If two logarithms of equal base are equal to each other, set the inputs equal to
each other and
solve.
With logarithmic equations (and some exponential equations), you must be aware
of extraneous solutions
– “solutions” that appear to be appear to be correct but don’t actually work out
in the original equation.
Homework problems:



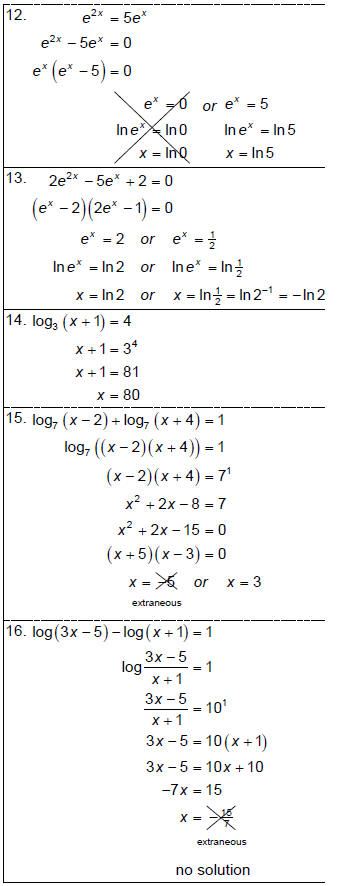
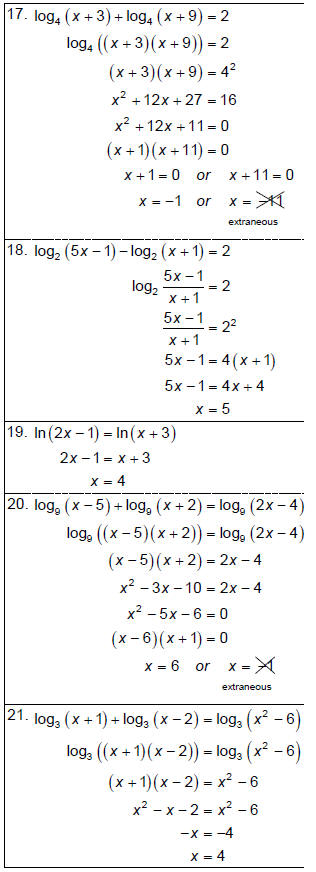
| Prev | Next |