Robot in a Maze
Instructions:
This project is to be done in groups of two or three students, as assigned by
the instructor.. Groups
of size four or more are not permitted. Each group will turn in one solution to
the tasks described below, and each
member of the group will receive the same grade on the project. You should be
careful to understand each part of
the project – related questions may appear on exams.
Submission Guidelines:
Please use the following guidelines when preparing your project for submission:
1. Include a cover page on which each member of the group signs their full
name. Also, in the top right hand
corner of each page submitted, write the names (first and last, written legibly)
of each group member. You
should not include student ID or social security numbers.
2. Only use one side of each sheet of paper and staple the pages together.
3. Presentation will be considered when grading this project. You should take
care to write legibly and hand in
full sheets of paper with no fringe, tears, etc. You should also clearly label
each problem and submit these in
order.
4. Give justification (in complete sentences!) for your answers
5. Be academically honest. This means, for example, providing a list of
sources other than the textbook (if any)
that you used to do the assignment; stating clearly that you’re copying or
mimicking an example from the book
in order to do the assignment (if appropriate).
6. The project is due at the beginning of class. Under certain circumstances,
late submissions may be accepted,
but they will be penalized.
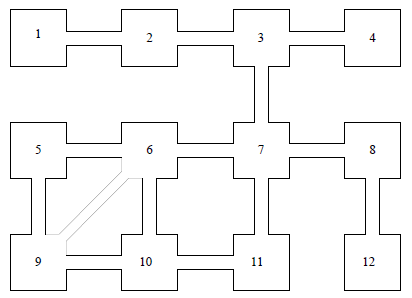
Setup: A robot is placed in the maze below and is programmed to move
at random. Each minute, the robot either
stays in the room it is currently located or chooses a hallway at random and
moves into the adjoining room, and
each possibility is equally likely . For example, if the robot happens to be in
room 11, then there is a 1/3 chance
it will move next to room 10, a 1/3 chance it will move next to room 7, and a
1/3 chance it will stay in room 11.
Project Tasks:
1. Find the appropriate transition matrix P for the Markov chain describing the movement of the robot.
2. Recall that a probability vector is a vector all of whose entries are
between 0 and 1 and such that the sum of
these entries is 1. Suppose v is probability vector in R12 whose i-th entry
gives the probability that the robot
is currently located in room i. What does the vector Pv tell you and why?
3. Carefully explain the real-world significance of the matrix P2. Be sure to
justify, in your own words, the
meaning of the entries of the matrix P2. It’s helpful to give explicit examples,
of the sort “The (3, 2) entry of
P2 tells me blah, blah, blah.” Do the same thing for P3, P4, etc.
4. An important concept in studying stochastic matrices is that of
“regularity”. A stochastic matrix is called
regular if some power of it has no zero entries. Show that P is regular. Also,
find the smallest integer k such
that Pk has no zero entries. What is the practical meaning (in terms of
properties of the maze) of this value
of k?
5. Calculate Pk for a very large value of k. (One fast way to do this is to
compute P2, P4, P8, etc. by repeatedly
squaring .) What do you notice about the entries of Pk for k very large?
6. What is the approximate probability that the robot will wind up in each of
the twelve rooms after a very long
time has passed? To answer this, it might help to use the answer to the previous
part, and to remember that
Pkej is the j-th column of Pk. Does your answer depend on where the robot begins
his journey?
7. Find a probability vector that solves the equation Px = x. This is called
a steady state vector for the system.
What’s the connection between this vector and your answer to the previous part?
8. What connection is there between the entries of the steady-state vector
and the nature of the maze? Can you
explain heuristically why some of the entries of the steady-state vector are
equal to others?
9. Suppose the maze is now modified so that the hallway joining rooms 3 and 7
is permanently blocked off. This
leads to a new transition matrix — call it Q. Is Q regular? How can you be sure
of your answer?
Computers:
You can conceivably do this project using just a fancy
calculator. I encourage you, however, to use the
software package Maple (or an equivalent one ). For one thing, it is far easier
to enter, manipulate, and view large
amounts of data in Maple than it is on a calculator, and this project will
require the use of rather large matrices.
Also, I believe it is a valuable experience to learn how to use a computer
algebra system such as Maple.
Maple is available on the Mathlab computer system and everyone in class should have access to Mathlab.
Here are some helpful tips concerning Maple. These are based on Version 10 of Maple
• You will need to “import” the linear algebra
package into Maple. Enter the command with (LinearAlgebra):
at the very start of your Maple session. (The trailing colon suppresses a long
list of commands that are imported
with the LinearAlgebra package — to see this list, replace the colon with a
semi-colon.)
• By default, Maple only displays in full matrices
of size at most 10 × 10. To increase this to 12, use
interface (rtablesize = 12);.
• To learn more about a Maple command or topic, type
in the command name or topic preceded by a question
mark. For example, try entering ?Matrix; into Maple. (You can also use the
menu-driven help documentation.)
• Here are a couple of useful commands:
– The command B := Matrix([[a,b,c],[d,e,f]]); sets
B to be the evident 2 × 3 matrix. Note that in
Maple, all commands should be ended with a “;” (or with a “:” if you don’t want
to see the output of the
command for some reason).
– You can use plus, minus, and exponents in the
usual manner for matrix operations. Instead of using an
asterisk for matrix multiplication , however, use the period key. For example,
enter A and B to be your
favorite 3 × 3 and 2 × 3 matrices, and try B.(A+3A^2);.
– The command ReducedRowEchelonForm(A); puts the matrix A in to reduced row echelon form.
– Suppose A is a matrix with rational numbers as
entries and you would rather have them as decimals.
Then you could use the command map(evalf,A);. Suppose you want to round off the
entries of A to 3
decimal places of accuracy. (This is useful for printing a large matrix so that
it fits on one page.) Then
use map(x -> evalf(x,3),A);.
| Prev | Next |