SOLVING EXPONENTIAL EQUATIONS

Problem 3:

Solve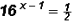

Method 1:

Let's use the natural logarithm in the solution process!

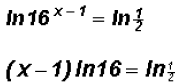Notice the parentheses around (x - 1)!!!

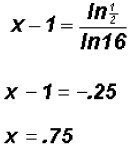
Method 2:

Please be aware that we can only use this method because the numbers
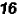
and 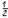have the same base when written in exponential form . That is,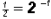
and .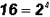

Therefore, let's rewrite 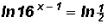as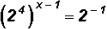

and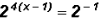

Since the two expressions are obviously equal, and the bases are also
obviously equal, then the two exponents also MUST be equal to each other.

Therefore,.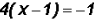

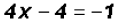
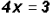and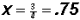

Problem 4:

Solve: 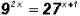not using logarithms !

Let's solve this exponential equation using the fact that 9 and 27 have the same base!
That is,

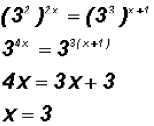
Problem 5:

Solve 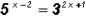. Round to 3 decimal places .

Let's use the common logarithm in the solution process !

Using the Power Rule we find

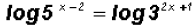
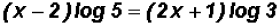
Next, we distribute the logarithmic expressions

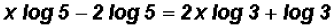
and collect the expressions containing the variable on one side

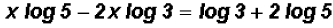
this allows us to factor out the variable and isolate it as follows

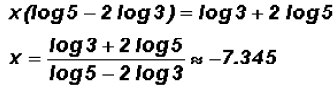
Problem 6:

How many years will it take for an initial investment of $10,000 to grow to $25,000?
Assume a rate of interest of 2.5% compounded continuously. Round your answer to a
whole number. Use the formula 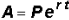, where P is the initial investment, A is the
accumulated amount, t is the time in years and r is the interest rate in decimals.

NOTE: Do not round until you find the final answer!

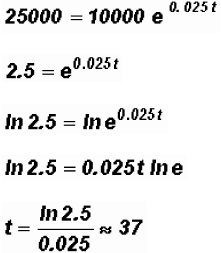
takes approximately 37 years for $10,000 to grow to $25,000 at a rate of
interest of 2.5%.

Problem 7:

The number of bacteria A in a certain culture is given by the growth model
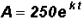. Find the growth constant k knowing that A = 280 when t = 5. Round
your answer to four decimal places.

NOTE: Do not round until you find the final answer!

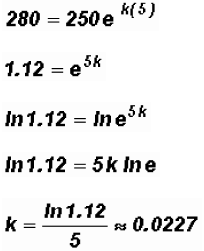
The growth constant k equals approximately 0.0227.

Problem 8:

The half-life of a radioactive substance is 950 years.. Find the constant k rounded to
seven decimal places. Do not use scientific notation! Hint: Half-life means that exactly
one-half of the original amount or size of the substance is left after a certain number of
years of growth/decay. Use the Exponential Growth /Decay Model 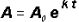, where
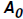is the original amount, A is the accumulated amount, t is the time in years and k is the
growth constant.

We know that after 950 years one-half of the original amount 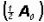is left. Therefore,

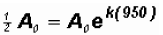
Then

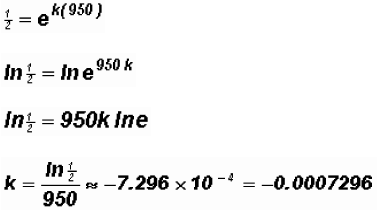
The decay constant k equals approximately - 0.0007296.

Problem 9:

The next problem involves carbon-14 dating which is used to determine the age of fossils
and artifacts. The method is based on considering the percentage of a half-life of carbon-
14 of approximately 5715 years. Specifically, the model for carbon-14 is

.

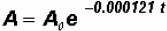In 1947, an Arab Bedouin herdsman found earthenware jars containing what are known
as the Dead Sea scrolls. Analysis at that time indicated that the scroll wrappings
contained 76% of their original carbon-14. Estimate the age of the scrolls in 1947.
Round your answer to a whole number.

We know that A, the amount present is 76% of the original amount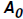 . Therefore, we
can use the model to write

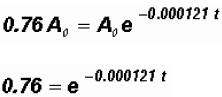
The Dead Sea Scrolls were approximately 2268 years old in 1947.